
【题目】如图是某种产品展开图,高为3cm.
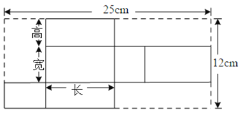
(1)求这个产品的体积.
(2)请为厂家设计一种包装纸箱,使每箱能装5件这种产品,要求没有空隙且要使该纸箱所用材料尽可能少(纸的厚度不计,纸箱的表面积尽可能小),求此长方体的表面积.
【答案】(1)长方形的体积为144cm3;(2)纸箱的表面积为516cm2.
【解析】
(1)根据已知图形得出长方体的高进而得出答案;
(2)设计的包装纸箱为15×6×8规格.
(1)长方体的高为3cm,则长方形的宽为(12-2×3)cm,长为![]() (25-3-6)cm,根据题意可得:
(25-3-6)cm,根据题意可得:
长方形的体积为:8×6×3=144(cm3);
(2)因为长方体的高为3cm,宽为6cm,长为8cm,
所以装5件这种产品,应该尽量使得6×8的面重叠在一起,纸箱所用材料就尽可能少,
这样的话,5件这种产品可以用15×6×8的包装纸箱,再考虑15×8的面积最大,所以15×8的面重叠在一起,纸箱所用材料就尽可能少,
所以设计的包装纸箱为15×6×8规格,该产品的侧面积分别为:
8×6=48(cm2),8×15=120(cm2),6×15=90(cm2)
纸箱的表面积为:2(120+48+90)=516(cm2).


科目:初中数学 来源: 题型:
【题目】我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.
(1)文学书和科普书的单价各多少钱?
(2)今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识背景)
据我国古代《周髀算经》记载,公元前1120年商高对周公说,将一根直尺折成一个直角,两端连接得到一个直角三角形,如果勾是3,股是4,那么弦就等于5,后人概括为“勾三、股四、弦五”.像3、4、5这样为三边长能构成直角三角形的三个正整数,称为勾股数.
(应用举例)
观察3,4,5;5,12,13;7,24,25;…
可以发现这些勾股数的勾都是奇数,且从3起就没有间断过,并且
勾为3时,股![]() ,弦
,弦![]() ;
;
勾为5时,股![]() ,弦
,弦![]() ;
;
请仿照上面两组样例,用发现的规律填空:
(1)如果勾为7,则股24= 弦25=
(2)如果勾用![]() (
(![]() ,且
,且![]() 为奇数)表示时,请用含有
为奇数)表示时,请用含有![]() 的式子表示股和弦,则股= ,弦= .
的式子表示股和弦,则股= ,弦= .
(解决问题)
观察4,3,5;6,8,10;8,15,17;…根据应用举例获得的经验进行填空:
(3)如果![]() 是符合同样规律的一组勾股数,
是符合同样规律的一组勾股数,![]() (
(![]() 表示大于1的整数),则
表示大于1的整数),则![]() ,
,![]() ,这就是古希腊的哲学家柏拉图提出的构造勾股数组的公式.
,这就是古希腊的哲学家柏拉图提出的构造勾股数组的公式.
(4)请你利用柏拉图公式,补全下面两组勾股数(数据从小到大排列)第一组: 、24、 :第二组: 、 、37.
查看答案和解析>>
科目:初中数学 来源: 题型:
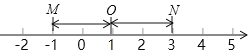
【题目】在数轴上,把表示数1的点称为基准点,记作点O,对于两个不同的点M和N,若点M、点N到点O的距离相等,则称点M与点N互为基准变换点.例如:图中,点M表示﹣1,点N表示3,它们与基准点O的距离都是2个单位长度,点M与点N互为基准变换点.对点A进行如下操作,先把点A表示的数乘以![]() ,再把所得数表示的点沿着数轴向左移动4个得长度得到点B,若点A与点B互为基准变换点,则点A表示的数为_____.
,再把所得数表示的点沿着数轴向左移动4个得长度得到点B,若点A与点B互为基准变换点,则点A表示的数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=![]() (a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在纸面上有一条数轴
![]()
操作一:
折叠数轴,使表示1的点与表示-1的点重合,则表示-5的点与表示 的点重合.
操作二:
折叠数轴,使表示1的点与表示3的点重合,在这个操作下回答下列问题:①表示-2的点与表示 的点重合;
②若数轴上A,B两点的距离为7(A在B的左侧),且折叠后A,B两点重合,则点A表示的数为 ,
点B表示的数为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠A=90°,AB=AC=![]() +2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
+2,D是边AC上的动点,BD的垂直平分线交BC于点E,连接DE,若△CDE为直角三角形,则BE的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com