
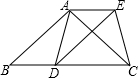
 已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.
已知:如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD,EC.分析 (1)利用等边对等角以及平行四边形的性质可以证得∠EDC=∠ACB,则易证△ADC≌△ECD,利用全等三角形的对应边相等即可证得;
(2)根据平行四边形性质推出AE=BD=CD,AE∥CD,得出平行四边形,根据AC=DE推出即可.
解答 (1)证明:∵AB=AC,
∴∠B=∠ACB,
又∵?ABDE中,AB=DE,AB∥DE,
∴∠B=∠EDC=∠ACB,AC=DE,
在△ADC和△ECD中,$\left\{\begin{array}{l}{AC=DE}&{\;}\\{∠EDC=∠ACB}&{\;}\\{DC=CD}&{\;}\end{array}\right.$,
∴△ADC≌△ECD(SAS).
(2)解:点D在BC的中点上时,四边形ADCE是矩形,理由如下:
∵四边形ABDE是平行四边形,
∴AE=BD,AE∥BC,
∵D为边长BC的中点,
∴BD=CD,
∴AE=CD,AE∥CD,
∴四边形ADCE是平行四边形,
∵△ADC≌△ECD,
∴AC=DE,
∴四边形ADCE是矩形.
点评 本题考查了平行四边形的性质以及等腰三角形的性质、全等三角形的判定与性质,矩形的判定的应用,证明两线段相等常用的方法就是转化为证两三角形全等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
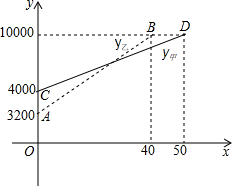 2016年国庆期间,某校准备组织部分教职工到黄山风景区旅游.经市场调研发现.如图,线段CD表示甲旅行社所需总费用y甲(元)与旅游人数x的函数图象,线段AB表示乙旅行社所需总费用y乙(元)与旅游人数x的函数图象,根据图象提供的信息,解答下列问题:
2016年国庆期间,某校准备组织部分教职工到黄山风景区旅游.经市场调研发现.如图,线段CD表示甲旅行社所需总费用y甲(元)与旅游人数x的函数图象,线段AB表示乙旅行社所需总费用y乙(元)与旅游人数x的函数图象,根据图象提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,△ABC的三个顶点坐标分别为(1,1)、(3,4)、(3,0).
在平面直角坐标系中,△ABC的三个顶点坐标分别为(1,1)、(3,4)、(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
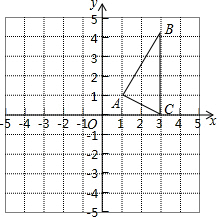
 如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.
如图,方格纸中每个小正方形的边长都是1个单位长度,△ABC在平面直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),( $\sqrt{2}$,$\sqrt{2}$ ),…,都是梦之点,显然梦之点有无数个.
在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),( $\sqrt{2}$,$\sqrt{2}$ ),…,都是梦之点,显然梦之点有无数个.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com