
【题目】某县政府计划拨款34000元为福利院购买彩电和冰箱,已知商场彩电标价为2000元/台,冰箱标价为1800元/台,如按标价购买两种家电,恰好将拨款全部用完.
(1)问原计划购买的彩电和冰箱各多少台?
(2)购买的时候恰逢商场正在进行促销活动,全场家电均降价![]() 进行销售,若在不增加县政府实际负担的情况下,能否比原计划多购买3台冰箱?请通过计算回答.
进行销售,若在不增加县政府实际负担的情况下,能否比原计划多购买3台冰箱?请通过计算回答.
【答案】(1)原计划购买彩电8台,购买冰箱10台;(2)在不增加县政府实际负担的情况下,能比原计划多购买3台冰箱,计算过程见解析
【解析】
(1)设原计划购买彩电x台,购买冰箱y台,根据题意列出二元一次方程,然后结合x、y的实际意义即可求出结论;
(2)先求出在购买台数不变的情况下,还剩多少元,即可判断结论.
解:(1)设原计划购买彩电x台,购买冰箱y台
由题意可得:2000x+1800y=34000,x、y均为正整数
解得:x=8,y=10
答:原计划购买彩电8台,购买冰箱10台.
(2)在购买台数不变的情况下,还剩34000×15%=5100(元)
现在每台冰箱售价为1800×(1-15%)=1530(元)
可买冰箱5100÷1530=3(台)……510(元)
答:在不增加县政府实际负担的情况下,能比原计划多购买3台冰箱.


科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,点E在边CD上,AQ⊥BE于点Q,DP⊥AQ于点P.
(1)求证:AP=BQ;
(2)在不添加任何辅助线的情况下,请直接写出图中四对线段,使每对中较长线段与较短线段长度的差等于PQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F.过点D作⊙O的切线交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.
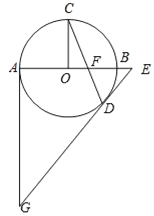
(1)求证:△EFD为等腰三角形;
(2)若OF:OB=1:3,⊙O的半径为3,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形![]() 中,
中,![]() 为直线
为直线![]() 上的点,
上的点,![]() 为直线
为直线![]() 上的点,分别连接
上的点,分别连接![]() ,
,![]() ,且
,且![]() .
.
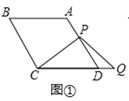
(1)若![]() ,点
,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 的延长线上,如图①,易证:
的延长线上,如图①,易证:![]() (不需证明);
(不需证明);
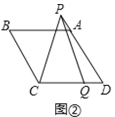
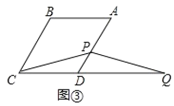
(2)如图②,若∠B=120°,点![]() 在线段
在线段![]() 上,点
上,点![]() 在线段
在线段![]() 的延长线上,如图③,猜想线段
的延长线上,如图③,猜想线段![]() ,
,![]() 和
和![]() 之间有怎样的数量关系?请直接写出对图②,图③的猜想,并选择其中一种情况给予证明.
之间有怎样的数量关系?请直接写出对图②,图③的猜想,并选择其中一种情况给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,且
的直径,且![]() ,点
,点![]() 为
为![]() 外一点,且
外一点,且![]() ,
,![]() 分别切
分别切![]() 于点
于点![]() 、
、![]() 两点.
两点.![]() 与
与![]() 的延长线交于点
的延长线交于点![]() .
.
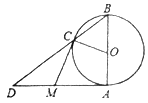
(1)求证:![]() ;
;
(2)填空
①当![]() ________时,四边形
________时,四边形![]() 是正方形.
是正方形.
②当![]() _________时,
_________时,![]() 为等边三角形.
为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,BC=AC,把△ABC绕点A按顺时针方向旋转45°后得到△AB’C’,若AB=2,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是___________ (结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)
我们知道若一个矩形是的周长固定,当相邻两边相等,即为正方形时,它的面积最大.反过来,若一个矩形的面积固定,它的周长是否会有最值呢?
(探究方法)
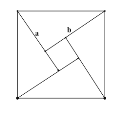
用两个直角边分别为![]() ,
,![]() 的4个全等的直角三角形可以拼成一个正方形。若
的4个全等的直角三角形可以拼成一个正方形。若![]() ,可以拼成如图所示的正方形,从而得到
,可以拼成如图所示的正方形,从而得到![]() ,即
,即![]() ;当
;当![]() 时,中间小正方形收缩为1个点,此时正方形的面积等于4个直角三角形面积的和.即
时,中间小正方形收缩为1个点,此时正方形的面积等于4个直角三角形面积的和.即![]() .于是我们可以得到结论:
.于是我们可以得到结论:![]() ,
,![]() 为正数,总有
为正数,总有![]() ,当且仅当
,当且仅当![]() 时,代数式
时,代数式![]() 取得最小值
取得最小值![]() .另外,我们也可以通过代数式运算得到类似上面的结论:
.另外,我们也可以通过代数式运算得到类似上面的结论:
∵![]() ,∴
,∴![]() ,
,![]()
∴对于任意实数![]() ,
,![]() 总有
总有![]() ,且当
,且当![]() 时,代数式
时,代数式![]() 取最小值
取最小值![]() .
.
使得上面的方法,对于正数![]() ,
,![]() ,试比较
,试比较![]() 和
和![]() 的大小关系.
的大小关系.
(类比应用)
利用上面所得到的结论完成填空
(1)当![]() 时,代数式
时,代数式![]() 有最 值为 .
有最 值为 .
(2)当![]() 时,代数式
时,代数式![]() 有最 值为 .
有最 值为 .
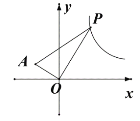
(3)如图,已知![]() 是反比例函数
是反比例函数![]() 图象上任意一动点,
图象上任意一动点,![]() ,
,![]() ,试求
,试求![]() 的最小面积.
的最小面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
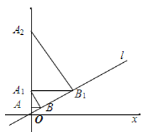
【题目】如图,已知直线l:y=![]() x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2020的坐标为______________.
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2020的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,过点A作⊙O的切线交BC的延长线于点D.
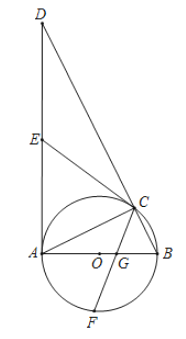
(1)求证:△DAC∽△DBA;
(2)过点C作⊙O的切线CE交AD于点E,求证:CE=![]() AD;
AD;
(3)若点F为直径AB下方半圆的中点,连接CF交AB于点G,且AD=6,AB=3,求CG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com