
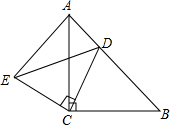
 如图,△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°,D在AB上.
如图,△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°,D在AB上. 解:(1)证明:如图,∵△ACB和△ECD均为等腰直角三角形,
解:(1)证明:如图,∵△ACB和△ECD均为等腰直角三角形,
|


科目:初中数学 来源: 题型:
 如图,△ABC是一块锐角三角形材料,边BC=40cm,高AD=30cm,要把它加工成矩形零件,矩形EFGH的一边FG在BC上,其余两个顶点分别在AB、AC上,AD与EH的交点为点M,设FG=x cm,当x为何值时,这个矩形零件的面积最大?最大面积是多少?
如图,△ABC是一块锐角三角形材料,边BC=40cm,高AD=30cm,要把它加工成矩形零件,矩形EFGH的一边FG在BC上,其余两个顶点分别在AB、AC上,AD与EH的交点为点M,设FG=x cm,当x为何值时,这个矩形零件的面积最大?最大面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:
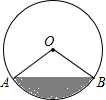 如图,有一个马戏帐篷,它的底部是圆形,其半径为20m,从a到b有一笔直的栅栏,其长为30m,观众在阴影区域里看马戏,如果每平方米可以坐三名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?
如图,有一个马戏帐篷,它的底部是圆形,其半径为20m,从a到b有一笔直的栅栏,其长为30m,观众在阴影区域里看马戏,如果每平方米可以坐三名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?查看答案和解析>>
科目:初中数学 来源: 题型:
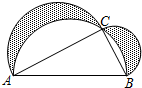 如图,班级美术课代表在办黑板报时设计了一个图案如图,在Rt△ABC中,∠C=90°,△ABC的面积为40cm2,在AB同侧分别以AB,BC,AC为直径作三个半圆,求阴影部分的面积.
如图,班级美术课代表在办黑板报时设计了一个图案如图,在Rt△ABC中,∠C=90°,△ABC的面积为40cm2,在AB同侧分别以AB,BC,AC为直径作三个半圆,求阴影部分的面积.查看答案和解析>>
科目:初中数学 来源: 题型:
 在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,CN,DM交于点O.
在?ABCD中,∠BCD和∠ADC的平分线分别交AB于M,N两点,CN,DM交于点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com