Question

9．⊙O中，直径长为10，弦AB∥CD，AB、CD长分别为6、8，则AB与CD的距离为7cm或1cm．

Answer 1

分析 分两种情况考虑：当两条弦位于圆心O一侧时，如图1所示，过O作OE⊥CD，交CD于点E，交AB于点F，连接OA，OC，由AB∥CD，得到OE⊥AB，利用垂径定理得到E与F分别为CD与AB的中点，在直角三角形AOF中，利用勾股定理求出OF的长，在三角形COE中，利用勾股定理求出OE的长，由OE-OF即可求出EF的长；当两条弦位于圆心O两侧时，如图2所示，同理由OE+OF求出EF的长即可．

解答 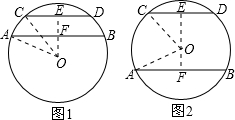解：分两种情况考虑：
当两条弦位于圆心O一侧时，如图1所示，
过O作OE⊥CD，交CD于点E，交AB于点F，连接OA，OC，
∵AB∥CD，∴OE⊥AB，
∴E、F分别为CD、AB的中点，
∴CE=DE=$\frac{1}{2}$CD=3cm，AF=BF=$\frac{1}{2}$AB=4cm，
在Rt△AOF中，OA=5cm，AF=4cm，
根据勾股定理得：OF=$\sqrt{{OA}^{2}-{AF}^{2}}$=3cm，
在Rt△COE中，OC=5cm，CE=3cm，
根据勾股定理得：OE=$\sqrt{{OC}^{2}-{CE}^{2}}$=4cm，
则EF=OE-OF=4-3=1cm；
当两条弦位于圆心O两侧时，如图2所示，同理可得EF=4+3=7cm，
综上，弦AB与CD的距离为7cm或1cm．
故答案为：7cm或1cm．

点评 此题考查了垂径定理，勾股定理，利用了分类讨论的思想，熟练掌握垂径定理是解本题的关键．