
【题目】平行四边形ABCD的两个顶点A、C在反比例函数y= ![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,AD交y轴于P点 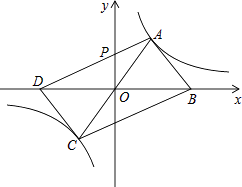
(1)已知点A的坐标是(2,3),求k的值及C点的坐标;
(2)在(1)的条件下,若△APO的面积为2,求点D到直线AC的距离.
【答案】
(1)解:∵点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数y= ![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,
∴3= ![]() ,点C与点A关于原点O对称,
,点C与点A关于原点O对称,
∴k=6,C(﹣2,﹣3),
即k的值是6,C点的坐标是(﹣2,﹣3);
(2)解:过点A作AN⊥y轴于点N,过点D作DM⊥AC,如图,
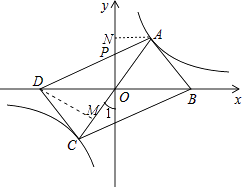
∵点A(2,3),k=6,
∴AN=2,
∵△APO的面积为2,
∴ ![]() ,
,
即 ![]() ,得OP=2,
,得OP=2,
∴点P(0,2),
设过点A(2,3),P(0,2)的直线解析式为y=kx+b,
![]() ,得
,得 ![]() ,
,
∴过点A(2,3),P(0,2)的直线解析式为y=0.5x+2,
当y=0时,0=0.5x+2,得x=﹣4,
∴点D的坐标为(﹣4,0),
设过点A(2,3),B(﹣2,﹣3)的直线解析式为y=mx+b,
则 ![]() ,得
,得 ![]() ,
,
∴过点A(2,3),C(﹣2,﹣3)的直线解析式为y=1.5x,
∴点D到直线AC的直线得距离为: ![]() =
= ![]() .
.
【解析】(1)根据点A的坐标是(2,3),平行四边形ABCD的两个顶点A、C在反比例函数y= ![]() (k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,可以求得k的值和点C的坐标;(2)根据△APO的面积为2,可以求得OP的长,从而可以求得点P的坐标,进而可以求得直线AP的解析式,从而可以求得点D的坐标,再根据点到直线的距离公式可以求得点D到直线AC的距离.
(k≠0)图象上,点B、D在x轴上,且B、D两点关于原点对称,可以求得k的值和点C的坐标;(2)根据△APO的面积为2,可以求得OP的长,从而可以求得点P的坐标,进而可以求得直线AP的解析式,从而可以求得点D的坐标,再根据点到直线的距离公式可以求得点D到直线AC的距离.
【考点精析】本题主要考查了平行四边形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,点![]() 在第一象限,过点A向x轴作垂线,垂足为点B,连接OA,
在第一象限,过点A向x轴作垂线,垂足为点B,连接OA,![]() ,点M从O出发,沿y轴的正半轴以每秒2个单位长度的速度运动,点N从点B出发以每秒3个单位长度的速度向x轴负方向运动,点M与点N同时出发,设点M的运动时间为t秒,连接AM,AN,MN.
,点M从O出发,沿y轴的正半轴以每秒2个单位长度的速度运动,点N从点B出发以每秒3个单位长度的速度向x轴负方向运动,点M与点N同时出发,设点M的运动时间为t秒,连接AM,AN,MN.
![]() 求a的值;
求a的值;
![]() 当
当![]() 时,
时,
![]() 请探究
请探究![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
![]() 试判断四边形AMON的面积是否变化?若不变化,请求出其值;若变化,请说明理由.
试判断四边形AMON的面积是否变化?若不变化,请求出其值;若变化,请说明理由.
![]() 当
当![]() 时,请求出t的值.
时,请求出t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数 ![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.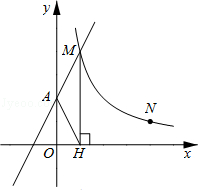
(1)求k的值;
(2)点N(a,1)是反比例函数 ![]() (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校兴趣小组对网上吐糟较为频繁的“医患关系”产生了兴趣,利用节假日在某社区开展了“造成医患关系紧张的原因”的问卷调查.
造成医患关系紧张的原因(单选) |
根据调查结果绘制出了如下两幅尚不完整的统计图.
根据以上信息解答下列问题:
(1)这次接受调查的总人数为人;
(2)在扇形统计图中,“A”所在扇形的圆心角的度数为;
(3)补全条形统计图;
(4)若该市有1000万人,请你估计选D的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“全民阅读”深入人心,读好书让人终身受益.为打造书香校园,满足同学们的读书需求,学校图书馆准备到新华书店采购文学名著和科技阅读两类图书.经了解,20本文学名著和40本科技阅读共需1520元,一本文学名著比一本科技阅读多22元(注:所采购的文学名著书价格都一样,所采购的科技阅读书价格都一样).
(1)求每本文学名著和科技阅读各多少元?
(2)若学校要求购买科技阅读比文学名著多20本,科技阅读和文学名著总数不低于72本,总费用不超过2000元,请你为学校求出符合条件的购书方案.
(3)请在(2)的条件下,请你求出此次活动学校最多需投入资金多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F
(1) 说明BE=CF的理由
(2) 如果AB=a,AC=b,求AE、BE的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚身高180cm,他站立在阳光下的影子长为90cm,他把手臂竖直举起,此时影子长为115cm,那么小刚的手臂超出头顶( )
A.35cm
B.50cm
C.25cm
D.45cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)问题发现
如图1,△ABC和△ADE均为等边三角形,点D在边BC上,连接CE.请填空:
①∠ACE的度数为;
②线段AC、CD、CE之间的数量关系为 . 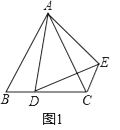
(2)拓展探究
如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在边BC上,连接CE.请判断∠ACE的度数及线段AC、CD、CE之间的数量关系,并说明理由.
(3)解决问题
如图3,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD=2,CD=1,AC与BD交于点E,请直接写出线段AC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3, ![]() ),点C的坐标为(
),点C的坐标为(![]() ,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
,0),点P为斜边OB上的一个动点,则PA+PC的最小值为( )
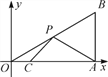
A. ![]() B.
B. ![]() C.
C. ![]() D. 2
D. 2 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com