
【题目】已知一次函数![]() 和二次函数
和二次函数![]() 部分自变量和对应的函数值如下表:
部分自变量和对应的函数值如下表:
| …… |
|
|
|
|
| …… |
| …… |
|
|
|
|
| …… |
| …… |
|
|
|
|
| …… |
(1)求![]() 的表达式;
的表达式;
(2)关于![]() 的不等式
的不等式![]() 的解集是 .
的解集是 .
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)根据题意设出y2的表达式,再把(0,0)代入,求出a的值,即可得出y2的表达式;
(2)利用表中数据得到直线与抛物线的交点为(-2,0)和(1,3),x<-2或x>1时,y2>y1,从而得出不等式ax2+bx+c>kx+m的解集.
解:(1)根据题意设y2的表达式为:
y2=a(x+1)2-1,
把(0,0)代入得a=1,
∴y2=x2+2x;
(2)当x=-2时,y1=y2=0;当x=1时,y1=y2=3;
∴直线与抛物线的交点为(-2,0)和(1,3),
而x<-2或x>1时,y2>y1,
∴不等式ax2+bx+c>kx+m的解集是x<-2或x>1.
故答案为:x<-2或x>1.


科目:初中数学 来源: 题型:
【题目】某酒店计划购买一批换气扇,已知购买2台![]() 型换气扇和2台
型换气扇和2台![]() 型换气扇共需220元;购买3台
型换气扇共需220元;购买3台![]() 型换气扇和1台
型换气扇和1台![]() 型换气扇共需200元.
型换气扇共需200元.
(1)求![]() 两种型号的换气扇的单价.
两种型号的换气扇的单价.
(2)若该酒店准备同时购进这两种型号的换气扇共60台,并且![]() 型换气扇的数量不多于
型换气扇的数量不多于![]() 型换气扇数量的2倍,请设计出最省钱的购买方案,并说明理由.
型换气扇数量的2倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
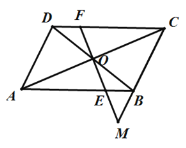
【题目】如图,ABCD的对角线AC,BD相交于点O,EF经过点O,分别交AB,CD于点E,F,FE的延长线交CB的延长线于点M.
(1)求证:OE=OF;
(2)若AD=4,AB=6,BM=1,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,过⊙T外一点P引它的两条切线,切点分别为M,N,若![]() ,则称P为⊙T的环绕点.
,则称P为⊙T的环绕点.
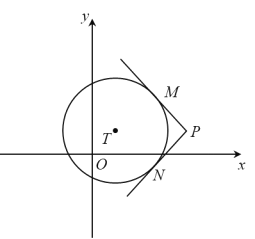
(1)当⊙O半径为1时,
①在![]() 中,⊙O的环绕点是___________;
中,⊙O的环绕点是___________;
②直线y=2x+b与x轴交于点A,y轴交于点B,若线段AB上存在⊙O的环绕点,求b的取值范围;
(2)⊙T的半径为1,圆心为(0,t),以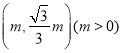 为圆心,
为圆心,![]() 为半径的所有圆构成图形H,若在图形H上存在⊙T的环绕点,直接写出t的取值范围.
为半径的所有圆构成图形H,若在图形H上存在⊙T的环绕点,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() .
.

(1)求抛物线的解析式;
(2)点![]() 为第一象限抛物线上一点,连接
为第一象限抛物线上一点,连接![]() 、
、![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(3)在(2)的条件下,点![]() 为第四象限抛物线上一点,连接
为第四象限抛物线上一点,连接![]() ,过点
,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,射线
,射线![]() 交第三象限抛物线于点
交第三象限抛物线于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
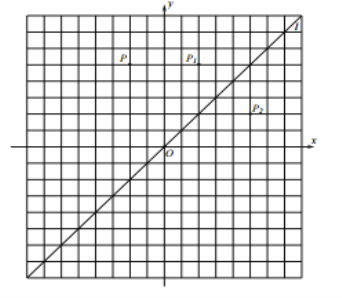
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 为一、三象限角平分线,点
为一、三象限角平分线,点![]() 关于
关于![]() 轴的对称点称为
轴的对称点称为![]() 的一次反射点,记作
的一次反射点,记作![]() ;
;![]() 关于直线
关于直线![]() 的对称点称为点
的对称点称为点![]() 的二次反射点,记作
的二次反射点,记作![]() .
.
例如,点![]() 的一次反射点为
的一次反射点为![]() ,二次反射点为
,二次反射点为![]() .
.
根据定义,回答下列问题:
(1)点![]() 的一次反射点为__________,二次反射点为____________;
的一次反射点为__________,二次反射点为____________;
(2)当点![]() 在第一象限时,点
在第一象限时,点![]() ,
,![]() ,
,![]() 中可以是点
中可以是点![]() 的二次反射点的是___________;
的二次反射点的是___________;
(3)若点![]() 在第二象限,点
在第二象限,点![]() ,
,![]() 分别是点
分别是点![]() 的一次、二次反射点,
的一次、二次反射点,![]() 为等边三角形,求射线
为等边三角形,求射线![]() 与
与![]() 轴所夹锐角的度数.
轴所夹锐角的度数.
(4)若点![]() 在
在![]() 轴左侧,点
轴左侧,点![]() ,
,![]() 分别是点
分别是点![]() 的一次、二次反射点,
的一次、二次反射点,![]() 是等腰直角三角形,请直接写出点
是等腰直角三角形,请直接写出点![]() 在平面直角坐标系
在平面直角坐标系![]() 中的位置.
中的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
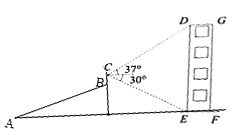
【题目】某同学利用数学知识测量建筑物DEFG的高度.他从点![]() 出发沿着坡度为
出发沿着坡度为![]() 的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端
的斜坡AB步行26米到达点B处,用测角仪测得建筑物顶端![]() 的仰角为37°,建筑物底端
的仰角为37°,建筑物底端![]() 的俯角为30°,若AF为水平的地面,侧角仪竖直放置,其高度BC=1.6米,则此建筑物的高度DE约为(精确到
的俯角为30°,若AF为水平的地面,侧角仪竖直放置,其高度BC=1.6米,则此建筑物的高度DE约为(精确到![]() 米,参考数据:
米,参考数据:![]() ,
,![]() )( )
)( )
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON及其边上一点A,以点A为圆心,AO长为半径画弧,分别交OM,ON于点B和C,再以点C为圆心,AC长为半径画弧,恰好经过点B,错误的结论是( ).
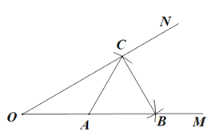
A.![]() B.∠OCB=90°C.∠MON=30°D.OC=2BC
B.∠OCB=90°C.∠MON=30°D.OC=2BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+2ax-3与x轴交于A、B(1,0)两点(点A在点B的左侧),与y轴交于点C,将抛物线沿y轴平移m(m>0)个单位,当平移后的抛物线与线段OA有且只有一个交点时,则m的取值范围是_______________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com