
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
分析 设方程${x^2}-\sqrt{2}bx+1=0$的两根为m、n,根据根与系数的关系得到m+n=$\sqrt{2}$b,mn=1,由|m-n|=2$\sqrt{5}$变形得到(m+n)2-4mn=20,则($\sqrt{2}$b)2-4=20,解得b=2$\sqrt{3}$或b=-2$\sqrt{3}$(舍去),如图,AB=AC=2,BC=2$\sqrt{3}$,作AD⊥BC于D,根据等腰三角形的性质得BD=$\frac{1}{2}$BC=$\sqrt{3}$,然后根据余弦的定义可求出∠B的度数.
解答 解:设方程${x^2}-\sqrt{2}bx+1=0$的两根为m、n,则m+n=$\sqrt{2}$b,mn=1,
而|m-n|=2$\sqrt{5}$,
所以(m-n)2=20,则(m+n)2-4mn=20,
($\sqrt{2}$b)2-4=20,解得b=2$\sqrt{3}$或b=-2$\sqrt{3}$(舍去),
所以等腰三角形三边的长为2、2、2$\sqrt{3}$,
如图, AB=AC=2,BC=2$\sqrt{3}$,
AB=AC=2,BC=2$\sqrt{3}$,
作AD⊥BC于D,则BD=$\frac{1}{2}$BC=$\sqrt{3}$,
所以cosB=$\frac{BD}{AB}$=$\frac{\sqrt{3}}{2}$,
所以∠B=30°.
故选A.
点评 本题考查了根与系数的关系:若二次项系数不为1,则常用以下关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了等腰三角形的性质.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BC为半⊙O的直径,D是弧CA的中点,连接OD,交AC于点F.
如图,BC为半⊙O的直径,D是弧CA的中点,连接OD,交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 7 | B. | -17 | C. | 14 | D. | -14 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
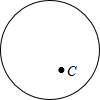 如图,已知⊙O的直径为10,点C是圆内一点,且OC=3.
如图,已知⊙O的直径为10,点C是圆内一点,且OC=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.
如图,A,B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离:现在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
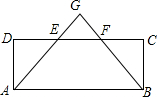 如图,在矩形ABCD中,E、F为边CD上的两点,且DE=EF=FC,连结AE、BF,并延长AE,BF相交于G
如图,在矩形ABCD中,E、F为边CD上的两点,且DE=EF=FC,连结AE、BF,并延长AE,BF相交于G查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com