


科目:初中数学 来源: 题型:

| 图形编号 | (1) | (2) | (3) | (4) | (5) | (6) |
| 圆的个数 | 1 |
4 |
9 |
16 |
25 |
36 |
查看答案和解析>>
科目:初中数学 来源: 题型:
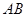 为18米,拱顶
为18米,拱顶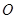 离水面
离水面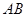 的距离
的距离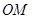 为8米,货船在水面上的部分的横断面是矩形
为8米,货船在水面上的部分的横断面是矩形 ,如图建立平面直角坐标系.
,如图建立平面直角坐标系.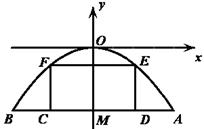
 的长为9米,
的长为9米,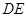 的长不能超过多少米,才能使船通过拱桥?
的长不能超过多少米,才能使船通过拱桥? ,请将矩形
,请将矩形 的面积
的面积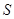 用含
用含 的代数式表示,并指出
的代数式表示,并指出 的取值范围.
的取值范围.查看答案和解析>>
科目:初中数学 来源:2013届八年级第二学期期中考试数学卷(解析版) 题型:解答题
(本大题10分)如果设f(x)= ,
那么f(a)表示当x=a时,
,
那么f(a)表示当x=a时, 的值,即f(a)=
的值,即f(a)= ,如:f(1)=
,如:f(1)= =
= .
.
(1)求f(2) +f ( )的值;
)的值;
(2)求f( )+f(
)+f( )的值;
)的值;
(3)计算: f(1)+f(2)+f( )+f(3)+f(
)+f(3)+f( )+…+f(n)+f(
)+…+f(n)+f( ).(结果用含有n的代数式表示,n为正整数)
).(结果用含有n的代数式表示,n为正整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com