
【题目】如图,在四边形ABCD中,AB=6,BC=8,CD=24,AD=26,∠B=90°,以AD为直径作圆O,过点D作DE∥AB交圆O于点E
(1)证明点C在圆O上;
(2)求tan∠CDE的值;
(3)求圆心O到弦ED的距离.
【答案】
(1)证明:如图1,
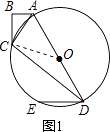
连结CO.
∵AB=6,BC=8,∠B=90°,
∴AC=10.
又∵CD=24,AD=26,102+242=262,
∴△ACD是直角三角形,∠C=90°.
∵AD为⊙O的直径,
∴AO=OD,OC为Rt△ACD斜边上的中线,
∴OC= ![]() AD=r,
AD=r,
∴点C在圆O上;
(2)解:如图2,

延长BC、DE交于点F,∠BFD=90°.
∵∠BFD=90°,
∴∠CDE+∠FCD=90°,
又∵∠ACD=90°,
∴∠ACB+∠FCD=90°,
∴∠CDE=∠ACB.
在Rt△ABC中,tan∠ACB= ![]() =
= ![]() ,
,
∴tan∠CDE=tan∠ACB= ![]() ;
;
(3)解:如图3,

连结AE,作OG⊥ED于点G,则OG∥AE,且OG= ![]() AE.
AE.
易证△ABC∽△CFD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴CF= ![]() ,
,
∴BF=BC+CF=8+ ![]() =
= ![]() .
.
∵∠B=∠F=∠AED=90°,
∴四边形ABFE是矩形,
∴AE=BF= ![]() ,
,
∴OG= ![]() AE=
AE= ![]() ,
,
即圆心O到弦ED的距离为 ![]() .
.
【解析】本题是圆的综合题,考查了勾股定理及其逆定理,直角三角形的性质,余角的性质,锐角三角函数定义,相似三角形的判定与性质,综合性较强,难度适中.准确作出辅助线,利用数形结合是解题的关键.(1)如图1,连结CO.先由勾股定理求出AC=10,再利用勾股定理的逆定理证明△ACD是直角三角形,∠C=90°,那么OC为Rt△ACD斜边上的中线,根据直角三角形斜边上的中线等于斜边的一半得出OC= ![]() AD=r,即点C在圆O上;(2)如图2,延长BC、DE交于点F,∠BFD=90°.根据同角的余角相等得出∠CDE=∠ACB.在Rt△ABC中,利用正切函数定义求出tan∠ACB=
AD=r,即点C在圆O上;(2)如图2,延长BC、DE交于点F,∠BFD=90°.根据同角的余角相等得出∠CDE=∠ACB.在Rt△ABC中,利用正切函数定义求出tan∠ACB= ![]() =
= ![]() ,则tan∠CDE=tan∠ACB=
,则tan∠CDE=tan∠ACB= ![]() ;(3)如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG=
;(3)如图3,连结AE,作OG⊥ED于点G,则OG∥AE,且OG= ![]() AE.易证△ABC∽△CFD,根据相似三角形对应边成比例求出CF=
AE.易证△ABC∽△CFD,根据相似三角形对应边成比例求出CF= ![]() ,那么BF=BC+CF=
,那么BF=BC+CF= ![]() .再证明四边形ABFE是矩形,得出AE=BF=
.再证明四边形ABFE是矩形,得出AE=BF= ![]() ,所以OG=
,所以OG= ![]() AE=
AE= ![]() .
.
【考点精析】通过灵活运用实数的运算,掌握先算乘方、开方,再算乘除,最后算加减,如果有括号,先算括号里面的,若没有括号,在同一级运算中,要从左到右进行运算即可以解答此题.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀.这次竞赛中甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如图所示.

(1)求出下列成绩统计分析表中![]() 的值;
的值;
(2)小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略上!”观察上面表格判断,小英是甲、乙哪个组的学生;
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组,但乙组同学不同意甲组同学的说法,认为他们的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是( ) 
A.π
B.![]()
C.3+π
D.8﹣π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】包装厂有42名工人,每人平均每天可以生产圆形铁片120片或长方形铁片80片.为了每天生产的产品刚好制成一个密封的圆桶,应该分配多少名工人生产圆形铁片,多少名工人生产长方形铁片?设应分配x名工人生产长方形铁片,(42-x)名工人生产圆形铁片,则下列所列方程正确的是( )
A. 120x=2×80(42-x) B. 80x=120(42-x)
C. 2×80x=120(42-x) D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,∠B=60°,点E在边BC上,点F在边CD上.
(1)如图①,若点E是BC的中点,∠AEF=60°,求证:BE=DF;
(2)如图②,若∠EAF=60°,求证:△AEF是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC边上的一点,E为AD的中点,过A作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少千米处?
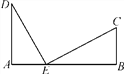
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级开展征文活动,征文主题只能从“爱国”“敬业”“诚信”“友善”四个主题选择一个,九年级每名学生按要求都上交了一份征文,学校为了解选择各种征文主题的学生人数,随机抽取了部分征文进行了调查,根据调查结果绘制成如下两幅不完整的统计图.

(1)求共抽取了多少名学生的征文;
(2)将上面的条形统计图补充完整;
(3)在扇形统计图中,选择“爱国”主题所对应的圆心角是多少;
(4)如果该校九年级共有1200名学生,请估计选择以“友善”为主题的九年级学生有多少名.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com