
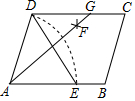
 如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( )
如图,在?ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
分析 连接EG,由作图可知AD=AE,根据等腰三角形的性质可知AG是DE的垂直平分线,由平行四边形的性质可得出CD∥AB,故可得出∠2=∠3,据此可知AD=DG,由等腰三角形的性质可知OA=$\frac{1}{2}$AG,利用勾股定理求出OA的长即可.
解答 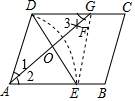 解:连接EG,
解:连接EG,
∵由作图可知AD=AE,AG是∠BAD的平分线,
∴∠1=∠2,
∴AG⊥DE,OD=$\frac{1}{2}$DE=3.
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠2=∠3,
∴∠1=∠3,
∴AD=DG.
∵AG⊥DE,
∴OA=$\frac{1}{2}$AG.
在Rt△AOD中,OA=$\sqrt{A{D}^{2}-O{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∴AG=2AO=8.
故选B.
点评 本题考查的是作图-基本作图,熟知角平分线的作法和性质是解答此题的关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:填空题
| 植树棵数 | 3 | 4 | 5 | 6 |
| 人数 | 20 | 15 | 10 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
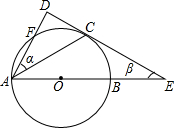 如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,过点A作切线DE的垂线,垂足为D,且与⊙O交于点F,设∠DAC,∠CEA的度数分别是α,β.
如图,AB是⊙O的直径,AC是上半圆的弦,过点C作⊙O的切线DE交AB的延长线于点E,过点A作切线DE的垂线,垂足为D,且与⊙O交于点F,设∠DAC,∠CEA的度数分别是α,β.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
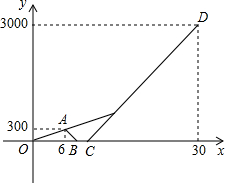 为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆.已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与出发的时间x(分钟)的函数图象,根据图象解答下列问题:
为营造书香家庭,周末小亮和姐姐一起从家出发去图书馆借书,走了6分钟忘带借书证,小亮立即骑路边共享单车返回家中取借书证,姐姐以原来的速度继续向前行走,小亮取到借书证后骑单车原路原速前往图书馆,小亮追上姐姐后用单车带着姐姐一起前往图书馆.已知单车的速度是步行速度的3倍,如图是小亮和姐姐距家的路程y(米)与出发的时间x(分钟)的函数图象,根据图象解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com