
【题目】某公司生产的某种产品每件成本为40元,经市场调查整理出如下信息:
①该产品90天售量(n件)与时间(第x天)满足一次函数关系,部分数据如下表:

②该产品90天内每天的销售价格与时间(第x天)的关系如下表:
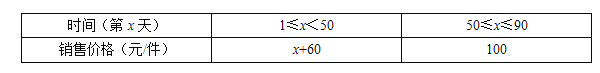
(1)求出第10天日销售量;
(2)设销售该产品每天利润为y元,请写出y关于x的函数表达式,并求出在90天内该产品的销售利润最大?最大利润是多少?(提示:每天销售利润=日销售量×(每件销售价格﹣每件成本))
(3)在该产品销售的过程中,共有多少天销售利润不低于5400元,请直接写出结果.
【答案】(1)180;(2)当x=40时,y的值最大,最大值是7200;(3)46天销售利润不低于5400元.
【解析】
(1)根据待定系数法解出一次函数解析式即可,进而得出第10天日销售量;
(2)当1≤x<50时,y=-2x2+160x+4000;当50≤x≤90时,y=-120x+12000,分别求出各段上的最大值,比较即可得到结论;
(3)根据1≤x<50和50≤x≤90时,由y≥5400求得x的范围,据此可得销售利润不低于5400元的天数.
解:(1)∵n与x成一次函数,
∴设n=kx+b,将x=1,n=198,x=3,n=194代入,得:
![]() ,
,
解得:.![]()
所以n关于x的一次函数表达式为n=﹣2x+200,
故第10天日销售量:n=﹣20+200=180(件);
(2)设销售该产品每天利润为y元,y关于x的函数表达式为:
![]() ,
,
当1≤x<50时,y=﹣2x2+160x+4000=﹣2(x﹣40)2+7200,
∵﹣2<0,
∴当x=40时,y有最大值,最大值是7200;
当50≤x≤90时,y=﹣120x+12000,
∵﹣120<0,
∴y随x增大而减小,即当x=50时,y的值最大,最大值是6000;
综上所述,当x=40时,y的值最大,最大值是7200,即在90天内该产品第40天的销售利润最大,最大利润是7200元;
(3)当1≤x<50时,由y≥5400可得﹣2x2+160x+4000≥5400,
解得:10≤x≤70,
∵1≤x<50,
∴10≤x<50;
当50≤x≤90时,由y≥5400可得﹣120x+12000≥5400,
解得:x≤55,
∵50≤x≤90,
∴50≤x≤55,
综上所述,10≤x≤55,
故在该产品销售的过程中,共有46天销售利润不低于5400元.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)认真观察,并在④后面的横线上写出相应的等式.
![]()
①1=1 ②1+2=![]() =3 ③1+2+3=
=3 ③1+2+3=![]() =6 ④ …
=6 ④ …
(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.
![]()
1=12②1+3=22③3+6=32④6+10=42⑤ …
(3)通过猜想,写出(2)中与第n个点阵相对应的等式 .
【答案】(1)10;(2)见解析;(3)![]()
【解析】试题分析:(1)根据①②③观察会发现第四个式子的等号的左边是1+2+3+4,右边分子上是(1+4)×4,从而得到规律;
(2)通过观察发现左边是10+15,右边是25即5的平方;
(3)过对一些特殊式子进行整理、变形、观察、比较,归纳出一般规律.
试题解析:(1)根据题中所给出的规律可知:1+2+3+4=![]() =10;
=10;
(2)由图示可知点的总数是5×5=25,所以10+15=52.
(3)由(1)(2)可知![]()
点睛:主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目中的难点.
【题型】解答题
【结束】
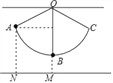
19
【题目】如图,用细线悬挂一个小球,小球在竖直平面内的A、C两点间来回摆动,A点与地面距离AN=14cm,小球在最低点B时,与地面距离BM=5cm,∠AOB=66°,求细线OB的长度.(参考数据:sin66°≈0.91,cos66°≈0.40,tan66°≈2.25)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】百日长跑为我校的传统项目,为了解九年级学生的体能状况,从我校九年级学生中随机抽取部分学生进行八百米跑体能测试,测试结果分为A、B、C、D四个等级,请根据两幅统计图中的信息回答下列问题:
![]() 求本次测试共调查了多少名学生?
求本次测试共调查了多少名学生?
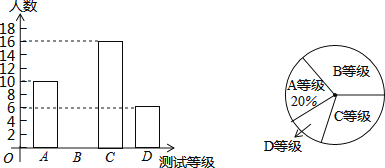
![]() 求本次测试结果为B等级的学生数,并补全条形统计图;
求本次测试结果为B等级的学生数,并补全条形统计图;
![]() 我校九年级共有2100名学生,请你估计九年级学生中体能测试结果为D等级的学生有多少人?
我校九年级共有2100名学生,请你估计九年级学生中体能测试结果为D等级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
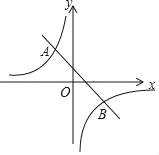
【题目】如图,已知A(m,2),B(2,n)是一次函数y=﹣x+1的图象与反比例函数y=![]() (k≠0)图象的两个交点.
(k≠0)图象的两个交点.
(1)求反比例函数的解析式;
(2)根据图象,请直接写出关于x的不等式﹣x+1<![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
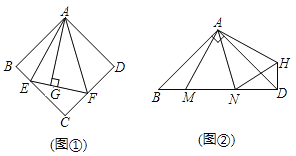
【题目】![]() 如图
如图![]() ,在正方形ABCD中,
,在正方形ABCD中,![]() 的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求
的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求![]() 的度数.
的度数.
![]() 如图
如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,点M,N是BD边上的任意两点,且
,点M,N是BD边上的任意两点,且![]() ,将
,将![]() 绕点A逆时针旋转
绕点A逆时针旋转![]() 至
至![]() 位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.
位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.
![]() 在图
在图![]() 中,连接BD分别交AE,AF于点M,N,若
中,连接BD分别交AE,AF于点M,N,若![]() ,
,![]() ,
,![]() ,求AG,MN的长.
,求AG,MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6cm,BC=12cm,∠B=90°.点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,设移动时间为t(s).

(1)当![]() 时,求△PBQ的面积;
时,求△PBQ的面积;
(2)当![]() 为多少时,四边形APQC的面积最小?最小面积是多少?
为多少时,四边形APQC的面积最小?最小面积是多少?
(3)当![]() 为多少时,△PQB与△ABC相似.
为多少时,△PQB与△ABC相似.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家销售一款商品,该商品的进价为每件80元,现在的售价为每件145元,每天可销售40件![]() 商场规定每销售一件需支付给商场管理费5元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件
商场规定每销售一件需支付给商场管理费5元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件![]() 若每件商品降价x元,每天的利润为y元,请完成以下问题的解答.
若每件商品降价x元,每天的利润为y元,请完成以下问题的解答.
![]() Ⅰ
Ⅰ![]() 用含x的式子表示:
用含x的式子表示:
![]() 每件商品的售价为______元;
每件商品的售价为______元;
![]() 每天的销售量为______件;
每天的销售量为______件;
![]() Ⅱ
Ⅱ![]() 求出y与x之间的函数关系式,并求出售价为多少时利润最大?最大利润是多少元?
求出y与x之间的函数关系式,并求出售价为多少时利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有3张背面相同的纸牌A,B,C,其正面分别画有三个不同的几何图形,

(1)求摸出一张纸片是中心对称图形的概率;
(2)将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张.求摸出两张牌面图形既是轴对称图形又是中心对称图形的纸牌的概率,(用树状图或列表法求解,纸牌可用A,B,C表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017四川省乐山市,第10题,3分)如图,平面直角坐标系xOy中,矩形OABC的边OA、OC分别落在x、y轴上,点B坐标为(6,4),反比例函数![]() 的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
的图象与AB边交于点D,与BC边交于点E,连结DE,将△BDE沿DE翻折至△B'DE处,点B'恰好落在正比例函数y=kx图象上,则k的值是( )
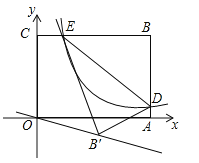
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com