
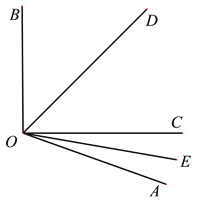
【题目】如图,∠AOB=110°,OD平分∠BOC,OE平分∠AOC。
(1)求∠EOD的度数。
(2)若∠BOC=90°,求∠AOE的度数。
【答案】(1)55゜, (2)10゜
【解析】试题分析:(1)根据OD平分∠BOC,OE平分∠AOC可知∠DOE=∠DOC+∠EOC=
![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB,由此即可得出结论;
∠AOB,由此即可得出结论;
(2)先根据∠BOC=90°求出∠AOC的度数,再根据角平分线的定义即可得出结论.
试题解析:(1)∵∠AOB=110°,OD平分∠BOC,OE平分∠AOC,
∴∠EOD=∠DOC+∠EOC=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB=
∠AOB=![]() ×110°=55°;
×110°=55°;
(2)∵∠AOB=110°,∠BOC=90°,
∴∠AOC=110°-90°=20°,
∵OE平分∠AOC,
∴∠AOE=![]() ∠AOC=
∠AOC=![]() ×1=20°=10°.
×1=20°=10°.


科目:初中数学 来源: 题型:
【题目】由于空气污染,气候干旱等因素,今年流感大肆流行,根据山东省卫计委统计,截止2018年1月,本年度全省共报告流感样病例442000例,其中0﹣14岁年龄组占到总病例数的88.09%,用科学记数法表示数字442000是( )
A. 4.42×103 B. 442×103 C. 4.42×105 D. 442×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N. 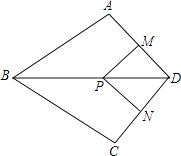
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH. 
(1)求证:∠APB=∠BPH;
(2)当点P在边AD上移动时,△PDH的周长是否发生变化?并证明你的结论;
(3)设AP为x,四边形EFGP的面积为S,求出S与x的函数关系式,试问S是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图像,解答下列问题: 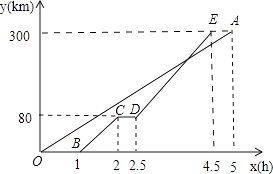
(1)线段CD表示轿车在中途停留了h;
(2)求轿车从甲地出发后经过多长时间追上货车.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两种机器人都被用来搬运化工原料,A型机器人比B型机器人每小时多搬运20千克,A型机器人搬运1000千克所用时间与B型机器人搬运800千克所用时间相等,两种机器人每小时分别搬运多少化工原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两厂在公路的同侧,现欲在公路边建一货场C.
(1)若要使货场到两厂的距离相等,请在图1中作出此时货场的位置.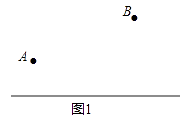
(2)若要求所修公路(即A、B两厂到货场的距离之和)最短,请在图2中作出货场的位置.(用尺规作图,保留作图痕迹,不必写作法)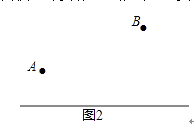
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,不正确的是( )
A.对角线相等的矩形是正方形B.对角线垂直平分的四边形是菱形
C.矩形的对角线平分且相等D.顺次连结菱形各边中点所得的四边形是矩形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com