
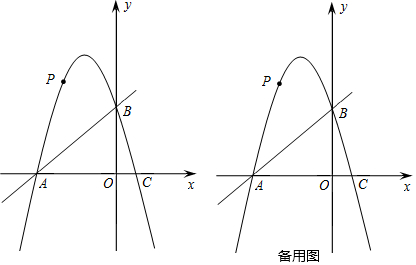
���� ��1�������Ա����뺯��ֵ�ö�Ӧ��ϵ���ɵ�A��B�����꣬���ݴ���ϵ�������ɵú�������ʽ��
��2������ƽ����y���ֱ���������ľ����ǽ������������С�������꣬�ɵ�PD�����ݶ��κ��������ʣ��ɵ�PD�����ֵ����������ĺͲ�ɵô𰸣�
��3�������������������ʣ��ɵù���x�ķ��̣����ݷ��̵Ľ�����ȵĶ�ʵ�������ɵ�n��ֵ�����ݽ��Ԫһ�η��̣��ɵô𰸣�
��� �⣺��1����y=x+3�У���x=0ʱ��y=3����y=0ʱ��x=-3��
���A��-3��0����B��0��3����
��������y=-x2+bx+c������A��B���㣬��
$\left\{\begin{array}{l}{c=3}\\{-9-3b+c=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=-2}\\{c=3}\end{array}\right.$��
�����ߵĽ���ʽΪy=-x2-2x+3��
��2����ͼ1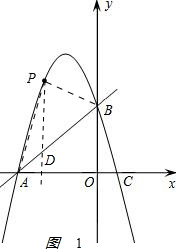 ������P��PD��x�ύAB��D�㣬
������P��PD��x�ύAB��D�㣬
�ߡ�ABC�������ȷ���ģ�
�൱��PAB��������ʱ���ı���PACB�����������߶�PD�ʱ����PAB��������
��P��m��-m2-2m+3����D��m��m+3����
PD=-m2-2m+3-��m+3��=-m2-3m=-��m+$\frac{3}{2}$��2+$\frac{9}{4}$��
�൱m=-$\frac{3}{2}$ʱ��PD�����ֵΪ$\frac{9}{4}$����m=-$\frac{3}{2}$ʱ��-m2-2m+3=$\frac{15}{4}$��
��P��-$\frac{3}{2}$��$\frac{15}{4}$����
��y=0ʱ��-x2-2x+3=0���x1=-3��x2=1��
��C��1��0����A��-3��0����
��C=1-��-3��=4��
���ı���PACB��������ֵΪ��$\frac{1}{2}$AC•OB+$\frac{1}{2}$PD•|xA|=$\frac{1}{2}$��4��3+$\frac{1}{2}$��$\frac{9}{4}$��3=6+$\frac{27}{8}$=$\frac{75}{8}$��
�൱��P������Ϊ��-$\frac{3}{2}$��$\frac{15}{4}$��ʱ���ı���PACB��������ֵ�������ֵΪ$\frac{75}{8}$��
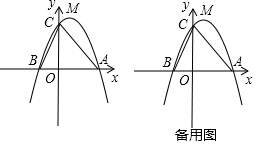
��3������A����P��ԭ����λ��ʱ�������ڷ�������ĵ�M���������£�
��ͼ2 ������P��PF��y����F�㣬����y���ϴ��ڵ�M��ʹ��PMA=90�㣬
������P��PF��y����F�㣬����y���ϴ��ڵ�M��ʹ��PMA=90�㣬
���PFM�ס�MOA����$\frac{PF}{MO}$=$\frac{FM}{OA}$��
��OM=x��FM=OF-OM=$\frac{15}{4}$-x����PF=$\frac{3}{2}$��OA=3��
��$\frac{\frac{3}{2}}{x}$=$\frac{\frac{15}{4}-x}{3}$�������
4x2-15x+18=0��
�ߡ�=b2-4ac=��-15��2-4��4��18=-63��0��
�÷�����ʵ���⣬
����ڵ�M��ʹ��PAM��Ϊ�Ե�MΪֱ�Ƕ����ֱ�������Σ�
�轫��A��Pͬʱ����ƽ��n����λ��ʹ֮�������⣬
����Ȼ����n=$\frac{3}{2}$ʱ����P����y���ϣ���ʱ��M����ԭ���غϣ���M1��0��0����
�ڵ�n=3ʱ����A��ԭ���غϣ�����P��y��Ĵ��ߣ�����ΪM����ʱM2��0��$\frac{15}{4}$����
�۵�M�ڣ�0��0���ͣ�0��$\frac{15}{4}$��֮��ʱ���轫��A����Pͬʱ����ƽ��n����λ���Ⱥ�A��P�Ķ�Ӧ�����A1��P1������P1��y��Ĵ���P1F������ΪF����ͼ3 ��
��
��ʱP1F=$\frac{3}{2}$-n��A1O=3-n��
��P1FM�ס�MOA1����$\frac{{P}_{1}F}{MO}$=$\frac{FM}{O{A}_{1}}$��
$\frac{\frac{3}{2}-n}{x}$=$\frac{\frac{15}{4}-x}{3-n}$������
4x2-15x+��4n2-18n+18��=0��
�ɵ�M��Ψһ�ԣ��÷�������ȵĶ�ʵ����
������-15��2-16��4n2-18n+18��=0��
���n1=$\frac{18+3\sqrt{29}}{8}$��n2=$\frac{18-3\sqrt{29}}{8}$��
��ʱ����4x2-15x+��4n2-18n+18��=0�Ľ�Ϊx1=x2=$\frac{15}{8}$��
��ʱM3��0��$\frac{15}{8}$����
�ཫ��A��Pͬʱ����ƽ��һ�����ȵ�λʱ�����ڷ��������ĵ�M����A��Pͬʱ����ƽ��$\frac{3}{2}$����λ����ʱ����M1��0��0��������A��Pͬʱ����ƽ��3����λ����ʱ��M2��0��$\frac{15}{4}$��������A��Pͬʱ����ƽ��$\frac{18��3\sqrt{29}}{8}$ʱ����M3��0��$\frac{15}{8}$����
���� ���⿼���˶��κ����ۺ��⣬�⣨1���Ĺؼ��Ǵ���ϵ�������⣨2���Ĺؼ�������ƽ����y���ֱ���������ľ����ǽ������������С��������ó�PD�����ֵ���⣨3���Ĺؼ����������������ε����ʵó�����x�ķ��̣��������˸����б�ʽ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �������� | ����ʱ�� | ����Ч�� | |
| �ƻ� | 1200 | $\frac{1200}{x}$ | x |
| ʵ�� | 1200 | $\frac{1200}{1.2x}$ | 1.2x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪�ڡ�ABC�У���D��E��F�ֱ���BC��AB��AC���ϣ�
��ͼ����֪�ڡ�ABC�У���D��E��F�ֱ���BC��AB��AC���ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���˺�����к������ֱ�����߹�ȥ | ����֮���߶���� |
| Ҫ���������Ӱ�ë���ܰ�װ��ǽ�� | ����ȷ��һ��ֱ�� |
| �Ž���ķ���ͨ���Ǵ�ֱ�ں����� | ������ƽ������߶��У����߶���� |
| ��ȥ�ӱߴ�ˮ���Ǵ�ֱ�ںӱ߷����� | ֱ����һ���ֱ���ϸ���������У����߶���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2x2 | B�� | 8x-2 | C�� | 2-8x | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 С��ȥ���а��������һ�����һ���Ļ��裮��ͼ������3���������һ��߶���9cm����8���������һ��߶���14cm������100���������һ��ʱ�����ĸ߶�Լ�ǣ�������
С��ȥ���а��������һ�����һ���Ļ��裮��ͼ������3���������һ��߶���9cm����8���������һ��߶���14cm������100���������һ��ʱ�����ĸ߶�Լ�ǣ�������| A�� | 116cm | B�� | 110cm | C�� | 114cm | D�� | 106cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪�ȱߡ�ABC��PΪAC�ӳ�����һ�㣬��PAΪ�����ȱߡ�APE��EC�ӳ��߽�BP��M������AM����֤��
��ͼ����֪�ȱߡ�ABC��PΪAC�ӳ�����һ�㣬��PAΪ�����ȱߡ�APE��EC�ӳ��߽�BP��M������AM����֤���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com