
【题目】综合与探究如图,在正方形![]() 中,点
中,点![]() 在
在![]() 边所在的直线上运动但不与点
边所在的直线上运动但不与点![]() 重合,点
重合,点![]() 在线段
在线段![]() .上运动,过点
.上运动,过点![]() 的直线
的直线![]() ,分别交
,分别交![]() 于点
于点![]() .
.
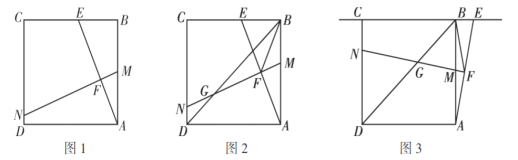
观察探究:(1)如图1,当点![]() 在边
在边![]() 上时,判断并说明
上时,判断并说明![]() 与
与![]() 的数量关系;
的数量关系;
探究发现:(2)勤奋小组在图1的基础上得到图2,点![]() 为
为![]() 中点时,其他条件不变,连接正方形的对角线
中点时,其他条件不变,连接正方形的对角线![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,此时,
,此时,![]() ,请利用图2证明;
,请利用图2证明;
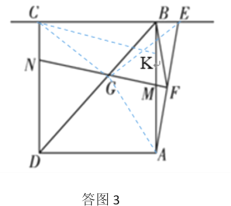
探究拓展:(3)如图3,缜密小组在勤奋小组的启发下,当点![]() 在点
在点![]() 右侧时,如果(2)中的其他条件不变,直线
右侧时,如果(2)中的其他条件不变,直线![]() 分别交直线
分别交直线![]() 于点
于点![]() ,他们发现线段
,他们发现线段![]() 与
与![]() 之间存在数量关系,线段
之间存在数量关系,线段![]() 与
与![]() 之间也存在数量关系,请你直接写出.
之间也存在数量关系,请你直接写出.
【答案】(1)AE=MN,理由见解析;(2)见解析;(3)![]() 与
与![]() 的数量关系是:
的数量关系是:![]() ,
,![]() 与
与![]() 的数量关系是:
的数量关系是:![]()
【解析】
(1)过点![]() 作
作![]() 交
交 ![]() 于点
于点![]() ,构建平行四边形PMND,再证明△ABE≌△DAP,即可得出结论;
,构建平行四边形PMND,再证明△ABE≌△DAP,即可得出结论;
(2)连接AG、EG、CG,构建全等三角形和直角三角形,证明AG=EG=CG,再根据四边形的内角和定理得∠AGE=90°,在Rt△ABE和Rt△AGE中,利用直角三角形斜边上的中线等于斜边的一半得BF=![]() AE,FG=
AE,FG=![]() AE,则BF=FG;
AE,则BF=FG;
(3)AE=MN,证明△AEB≌ONMQ; BF=FG,同理得出BF和FG分别是直角△AEB和直角△AGE斜边.上的中线,则BF=![]() AE,FG=
AE,FG=![]() AE,所以BF=FG.
AE,所以BF=FG.
解:(1)![]()
理由如下:如答图 1,过点![]() 作
作![]() 交
交 ![]() 于点
于点![]() ,则
,则![]()
![]() 四边形
四边形![]() 是正方形,
是正方形,
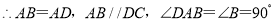
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形, ![]()
![]()
![]() 于
于![]()
![]()
又![]()
![]()
![]()
(2)如答图 2,连接![]()
由正方形的轴对称性得:![]()
![]()
![]() 于点
于点![]() ,点
,点![]() 为
为 ![]() 中点,
中点,![]()
![]()
![]()
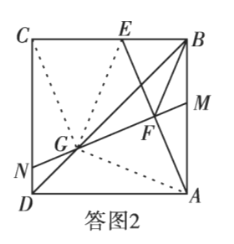
由答图 2 可知![]()
![]()
又![]() 四边形
四边形![]() 的内角和为
的内角和为![]()
![]()
在![]() 和
和![]() 中,
中,![]() 为斜边,点
为斜边,点 ![]() 为
为![]() 的中点
的中点
![]()
![]()
(3)AE与MN的数量关系是:AE=MN,理由是:
如图3,过C作CK∥MN交AB于K,
∴∠CKB=∠NMB=∠FMA
又∵正方形ABCD∴AB∥CD,AB=BC, ∠ABC=∠ABE=90°
∴四边形CNMK是平行四边形,∴CK=MN
∵MN⊥EF∴∠FMA+∠MAF=90°
∵∠BEA+∠MAF=90°
∴∠BEA=∠FMA=∠NMB=∠CKB
∴△CBK≌△ABE
∴AE=CK∴AE=MN
![]() 与
与![]() 的数量关系是:
的数量关系是:![]() 理由是:
理由是:
连接CG、AG、EG,
由正方形的轴对称性得:![]()
![]()
![]() 于点
于点![]() ,点
,点![]() 为
为 ![]() 中点,
中点,![]()
![]()
![]()
在Rt△ABE中,∠AEB+∠EAB=90°,即∠BAE+∠GEA+∠GEB=90°
∴∠BAE+∠GEA+∠GAB=90°∴∠GEA+∠GAE=90°
∵∠GEA+∠GAE+∠EGA=180°
∴∠EGA=90°
在![]() 和
和![]() 中,
中,![]() 为斜边,点
为斜边,点 ![]() 为
为![]() 的中点
的中点
![]()
![]()


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
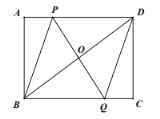
【题目】如图,矩形![]() 中,点
中,点![]() 是线段
是线段![]() 上一动点,
上一动点, ![]() 为
为![]() 的中点,
的中点, ![]() 的延长线交BC于
的延长线交BC于![]() .
.
(1)求证: ![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 从点
从点![]() 出发,以l
出发,以l![]() 的速度向
的速度向![]() 运动(不与
运动(不与![]() 重合).设点
重合).设点![]() 运动时间为
运动时间为![]() ,请用
,请用![]() 表示
表示![]() 的长;并求
的长;并求![]() 为何值时,四边形
为何值时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC,BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°.

(1)求证:四边形ABCD是矩形;
(2)若∠ADF:∠FDC=3:2,DF⊥AC,求∠BDF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
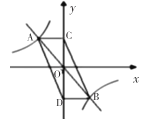
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,过
两点,过![]() 、
、![]() 两点分别作
两点分别作![]() 轴的垂线,垂足分别为点
轴的垂线,垂足分别为点![]() 、
、![]() ,连接
,连接![]() 、
、![]() ,则四边形
,则四边形![]() 的面积为( )
的面积为( )
A.4B.8C.12D.24
查看答案和解析>>
科目:初中数学 来源: 题型:
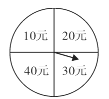
【题目】“十·一”期间,某服装店为了吸引更多的顾客购买服装,在.店门口设计了一个转转盘促销活动:当顾客转动转盘,根据指针指示返还相应的现金,若指针指在分界线时,需要重新转动,直到指向数字为止,购买几件服装就转动几次转盘.李女士购买了两件服装,她得到返还的现金数不低于![]() 元的概率是__________.
元的概率是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
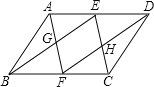
【题目】如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,连接AF、BE交于点G,连接CE、DF交于点H.
(1)求证:四边形EGFH为平行四边形;
(2)当AB与BC满足什么条件时,四边形EGFH为矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
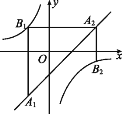
【题目】如图,已知点A1,A2,…,An均在直线![]() 上,点B1,B2,…,Bn均在双曲线
上,点B1,B2,…,Bn均在双曲线![]() 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为
上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为![]() (n为正整数).若
(n为正整数).若![]() ,则
,则![]() __,
__,![]() __.
__.
查看答案和解析>>
科目:初中数学 来源: 题型:
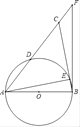
【题目】如图,在等腰△ABC中,AB=BC,以AB为直径的半圆分别交AC、BC于点D、E两点,BF与⊙O相切于点B,交AC的延长线于点F.
(1)求证:D是AC的中点;
(2)若AB=12,sin∠CAE=![]() ,求CF的值.
,求CF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并按要求解决问题:
问题:“在平面内,已知分别有2个点,3个点,4个点,5个点,…,![]() 个点,其中任意三个点都不在同一条直线上经过每两点画一条直线,它们可以分别画多少条直线?”
个点,其中任意三个点都不在同一条直线上经过每两点画一条直线,它们可以分别画多少条直线?”
探究:为了解决这个问题,希望小组的同学们,设计了如下表格进行探究:(为了方便研究问题,图中每条线段表示过线段两端点的一条直线)
点数 | 2 | 3 | 4 | 5 | … |
|
示意图 |
|
|
|
| … |
|
直线条数 | 1 |
|
|
| … |
请解答下列问题:
(1)请帮助希望小组归纳,并直接写出结论:当平面内有![]() 个点时,直线条数为______;
个点时,直线条数为______;
(2)若某同学按照本题中的方法,共画了28条直线,求该平面内有多少个已知点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com