
如图,在直角坐标系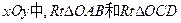 的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
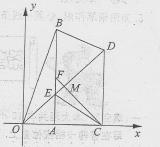
试解决下列问题:
(1)填空:点D坐标为 ;
(2)设点B横坐标为t,请把BD长表示成关于t的函数关系式,并化简;
(3)等式BO=BD能否成立?为什么?
(4)设CM与AB相交于F,当△BDE为直角三角形时,判断四边形BDCF的形状,并证明你的结论.
(1)
(2)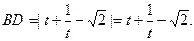
(3)略
(4)略
解析(1) ;(1分)
;(1分)
(2)
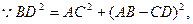
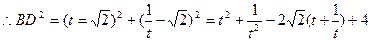 ① (2分)
① (2分) (3分)
(3分)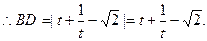 ② (4分)(注:不去绝对值符号不扣分)
② (4分)(注:不去绝对值符号不扣分)
(3)[法一]若OB=BD,则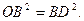
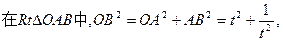
由①得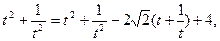 (5分)
(5分)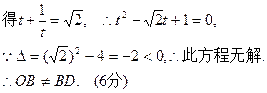
[法二]若OB=BD,则B点在OD的中垂线CM上.
∴直线CM的函数关系式为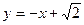 , ③ (5分)
, ③ (5分)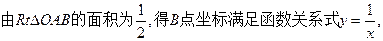 ④
④
联立③,④得: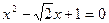 ,
,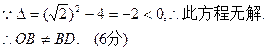
[法三]若OB=BD,则B点在OD的中垂线CM上,如图27 – 1
过点B作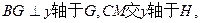
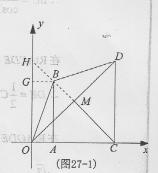
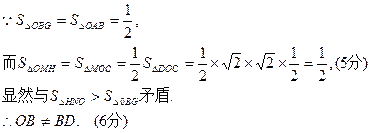
(4)如果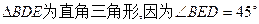 ,
,
①当 ,如图27 – 2
,如图27 – 2 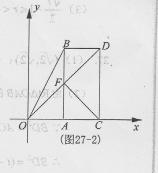
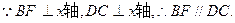
∴此时四边形BDCF为直角梯形.(7分)
②当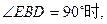 如图27 – 3
如图27 – 3 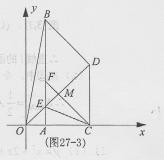
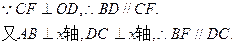
∴此时四边形BDCF为平行四边形.(8分)
下证平行四边形BDCF为菱形:
[法一]在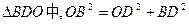 ,
,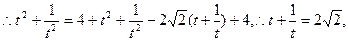
[方法①]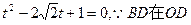 上方
上方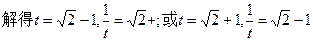 (舍去).
(舍去).
得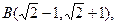
[方法②]由②得: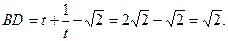
此时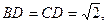
∴此时四边形BDCF为菱形(9分)
[法二]在等腰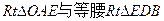 中
中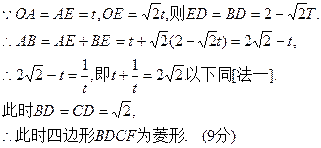


科目:初中数学 来源: 题型:
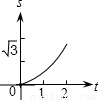
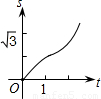
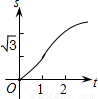
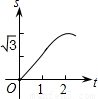
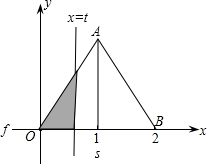 如图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是( )
如图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t(0≤t≤2)截这个三角形所得位于直线左侧的图形(阴影部分)的面积为f(t),则函数s=f(t)的图象只可能是( )A、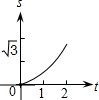 | B、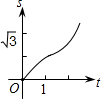 | C、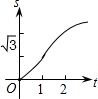 | D、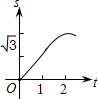 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标系的第一象限内,等边△ABO的边长为2,O为坐标原点,平行于y轴的动直线m沿OB方向平行移动,且与x轴相交于点D(x,0)(0≤x≤2),直线m截△ABO得直线m左侧的部分图形的面积y,那么y与x的函数关系图象大致是( )
如图,在直角坐标系的第一象限内,等边△ABO的边长为2,O为坐标原点,平行于y轴的动直线m沿OB方向平行移动,且与x轴相交于点D(x,0)(0≤x≤2),直线m截△ABO得直线m左侧的部分图形的面积y,那么y与x的函数关系图象大致是( )A、 | B、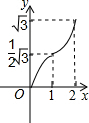 | C、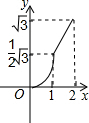 | D、 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在直角坐标系![]() 的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,
的直角顶点A,C始终在x轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,![]()
试解决下列问题:
(1)填空:点D坐标为 ;
(2)设点B横坐标为t,请把BD长表示成关于t的函数关系式,并化简;
(3)等式BO=BD能否成立?为什么?
(4)设CM与AB相交于F,当△BDE为直角三角形时,判断四边形BDCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2008年江苏省淮安市淮阴中学高中招生考试数学试卷(解析版) 题型:选择题
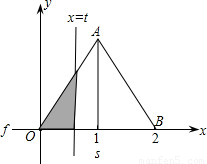
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com