
分析 根据分母有理化的一般步骤计算即可.
解答 解:(1)$\frac{1}{3\sqrt{2}}$=$\frac{\sqrt{2}}{3\sqrt{2}×\sqrt{2}}$=$\frac{\sqrt{2}}{6}$,
(2)$\frac{1}{\sqrt{12}}$=$\frac{\sqrt{3}}{\sqrt{12}×\sqrt{3}}$=$\frac{\sqrt{3}}{6}$,
(3)$\frac{\sqrt{10}}{2\sqrt{5}}$=$\frac{\sqrt{10}×\sqrt{5}}{2\sqrt{5}×\sqrt{5}}$=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{6}$;$\frac{\sqrt{3}}{6}$;$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分母有理化,分母有理化是指把分母中的根号化去,分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式.


科目:初中数学 来源: 题型:选择题
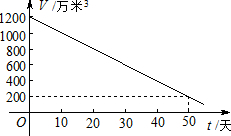 由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示,则下列说法正确的是( )
由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量V(万米3)与干旱的时间t(天)的关系如图所示,则下列说法正确的是( )| A. | 干旱第50天时,蓄水量为1200万米3 | |
| B. | 干旱开始后,蓄水量每天增加20万米3 | |
| C. | 干旱开始时,蓄水量为200万米3 | |
| D. | 干旱开始后,蓄水量每天减少20万米3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>$\frac{2}{3}$且x≠3 | B. | x≥$\frac{2}{3}$ | C. | x≥$\frac{2}{3}$且x≠3 | D. | x≤$\frac{2}{3}$且x≠-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
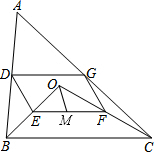 如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.
如图,点O是△ABC内一点,连结OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连结,得到四边形DEFG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
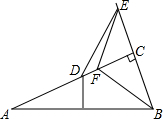 如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.
如图,在Rt△ABC中,∠ACB=90°,∠A=22.5°,斜边AB的垂直平分线交AC于点D,点F在AC上,点E在BC的延长线上,CE=CF,连接BF,DE.线段DE和BF在数量和位置上有什么关系?并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com