
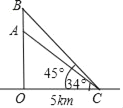
【题目】如图,一枚运载火箭从距雷达站C处5km的地面O处发射,当火箭到达点A,B时,在雷达站C处测得点A,B的仰角分别为34°,45°,其中点O,A,B在同一条直线上.求AC和AB的长(结果保留小数点后一位)(参考数据:sin34°≈0.56;cos34°≈0.83;tan34°≈0.67)
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】温度与我们的生活息息相关,如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(℉).设摄氏温度为x(℃)华氏温度为y(℉),则y是x的一次函数,通过观察我们发现,温度计上的摄氏温度为0℃时,华氏温度为32℉;摄氏温度为﹣20℃时,华氏温度为﹣4℉

请根据以上信息,解答下列问题
(1)仔细观察图中数据,试求出y与x的函数关系式;
(2)当摄氏温度为﹣5℃时,华氏温度为多少?
(3)当华氏温度为59℉时,摄氏温度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这
个分式为“和谐分式”.
(1)下列分式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④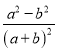 . 其中是“和谐分式”是 (填写序号即可);
. 其中是“和谐分式”是 (填写序号即可);
(2)若![]() 为正整数,且
为正整数,且![]() 为“和谐分式”,请写出
为“和谐分式”,请写出![]() 的值;
的值;
(3)在化简![]() 时,
时,
小东和小强分别进行了如下三步变形:
小东: ![]()
![]()

小强: ![]()
![]()
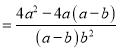
显然,小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单,
原因是: ,
请你接着小强的方法完成化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,AB=6cm,AD=24cm,BC与CD的长度之和为34cm,其中C是直线l上的一个动点,请你探究当C离点B有多远时,△ACD是以DC为斜边的直角三角形.
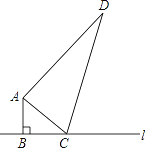
查看答案和解析>>
科目:初中数学 来源: 题型:
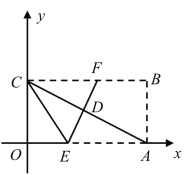
【题目】如图,把长方形纸片![]() 放入平面直角坐标系中,使
放入平面直角坐标系中,使![]() 分别落在
分别落在![]() 轴的的正半轴上,连接
轴的的正半轴上,连接![]() ,且
,且![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)将纸片![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合(折痕为
重合(折痕为![]() ),求折叠后纸片重叠部分
),求折叠后纸片重叠部分![]() 的面积;
的面积;
(3)求![]() 所在直线的函数表达式,并求出对角线
所在直线的函数表达式,并求出对角线![]() 与折痕
与折痕![]() 交点
交点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
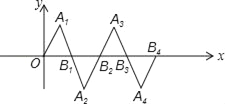
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
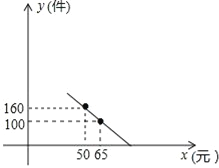
【题目】某商场老板对一种新上市商品的销售情况进行记录,已知这种商品进价为每件40元,经过记录分析发现,当销售单价在40元至90元之间(含40元和90元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.
(1)求y与x的函数关系式.
(2)设商场老板每月获得的利润为P(元),求P与x之间的函数关系式;
(3)如果想要每月获得2400元的利润,那么销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.

(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十字相乘法”能把二次三项式分解因式,对于形如ax2+bxy+cy2的关于x,y的二次三项式来说,方法的关键是把x2项系数a分解成两个因数a1,a2的积,即a=a1a2,把y2项系数c分解成两个因数c1,c2的积,即c=c1c2,并使a1c2+a2c1正好等于xy项的系数b,那么可以直接写成结果:ax2+bxy+cy2=(a1x+c1y)(a2x+c2y).
例:分解因式:x2﹣2xy﹣8y2.
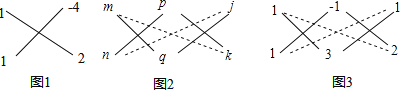
解:如图1,其中1=1×1,﹣8=(﹣4)×2,而﹣2=1×2+1×(﹣4).
∴x2﹣2xy﹣8y2=(x﹣4y)(x+2y)
而对于形如ax2+bxy+cy2+dx+ey+f的x,y的二元二次式也可以用十字相乘法来分解,如图2,将a分解成mn乘积作为一列,c分解成pq乘积作为第二列,f分解成jk乘积作为第三列,如果mq+np=b,pk+qj=e,mk+nj=d,即第1,2列、第2,3列和第1,3列都满足十字相乘规则,则原式=(mx+py+j)(nx+qy+k);
例:分解因式:x2+2xy﹣3y2+3x+y+2
解:如图3,其中1=1×1,﹣3=(﹣1)×3,2=1×2;
而2=1×3+1×(﹣1),1=(﹣1)×2+3×1,3=1×2+1×1;
∴x2+2xy﹣3y2+3x+y+2=(x﹣y+1)(x+3y+2)
请同学们通过阅读上述材料,完成下列问题:
(1)分解因式:
①6x2﹣17xy+12y2=
②2x2﹣xy﹣6y2+2x+17y﹣12=
③x2﹣xy﹣6y2+2x﹣6y=
(2)若关于x,y的二元二次式x2+7xy﹣18y2﹣5x+my﹣24可以分解成两个一次因式的积,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com