练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．大于-2.6而不大于$\sqrt{11}$的整数共有（　　）
    A．7个B．6个C．5个D．4个

    分析 先依据被开放数越大对应的算术平方根越大估算出$\sqrt{11}$的大小，然后找出符合题意的整数即可．

    解答 解：∵9＜11＜16，
    ∴3＜$\sqrt{11}$＜4．
    ∴大于-2.6而不大于$\sqrt{11}$的整数有：-2，-1，0，1，2，3，共6个．
    故选：B．

    点评 本题主要考查的是估算无理数的大小，求得$\sqrt{11}$的大致范围是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    5．某校初三学生开展毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间内每踢100个（含100）为优秀．下表是成绩最好的甲班和乙班各5名学生的比赛数据（单位：个）
    1号2号3号4号5号总分
    甲班1009811089103500
    乙班891009511997500
    经统计发现两班总分相等，此时有学生建议，可以通过考查数据中的其他信息作为参考．请你回答下列问题：
    （1）计算两班的优秀率及比赛数据的中位数；
    （2）哪一个班级学生的比赛成绩相互之间更接近，为什么？
    （3）根据以上信息，你认为应该把冠军奖状发给哪一个班级？说明理由！

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

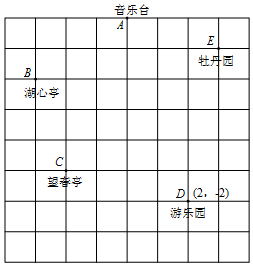    6．小王到公园游玩，回到家后，她利用平面直角坐标系画出了公园的景区地图，如图所示，可是她忘记了在图中标出原点和x轴、y轴，只知道游乐园D的坐标为（2，-2），且一格表示一个单位长度．
    （1）在原图中建立直角坐标系，求出其它各景点的坐标；
    （2）在（1）的基础上，记原点为0，分别表示出线段AO和线段DO上任意一点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．（1）计算：①$\sqrt{12}$-$\sqrt{18}$-$\sqrt{0.5}$+$\sqrt{\frac{1}{3}}$；    
     ②$\frac{1}{\sqrt{2}-1}$-$\sqrt{6}$÷$\sqrt{3}$-（2$\sqrt{3}$）2
    （2）解方程：①（y-2）（y+1）=y+1；  
    ②（x-5）（3x-2）=10．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．有下列说法：①任何无理数都是无限不循环小数；②在1和3之间的无理数有且只有$\sqrt{2}；\sqrt{3}；\sqrt{5}；\sqrt{7}$这4个；③1的立方根与平方根都是1；④$\frac{π}{2}$是分数；⑤估计$\sqrt{31}$-1的值是在4和5之间；其中正确的个数是（　　）
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．数据0.000000062用科学记数法可表示为（　　）
    A．6.2×10-7B．6.2×10-8C．6.2×10-9D．6.2×10-10

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

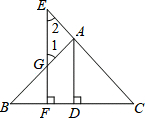    7．已知：如图，AD⊥BC于D，EF⊥BC于F，交AB于G，交CA延长线于E，∠1=∠2．
    求证：AD平分∠BAC．
    证明：∵AD⊥BC，EF⊥BC（已知）
    ∴∠EFC=∠ADC=90°（垂直的定义）
    ∴EF∥AD（同位角相等，两直线平行）
    ∴∠1=∠BAD（两直线平行，内错角相等）
    ∠2=∠DAC（两直线平行，同位角相等）
    ∵∠1=∠2（已知）
    ∴∠DAC=∠DAB（等量代换）
    即AD平分∠BAC（角平分线的定义）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．已知$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$是二元一次方程2x+ay=4的一个解，则a的值为（　　）
    A．2B．-2C．1D．-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

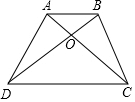    5．如图，在梯形ABCD中，AB∥CD，若AB=1，DC=2，那么①△ABO∽△CDO；②△ADO∽△BCO；③△ABO与△ADO的面积比是1：2．上述三个结论中正确的是（　　）
    A．①②B．①③C．②③D．①②③

    查看答案和解析>>

    同步练习册答案