
【题目】如图所示,AD∥BC,∠ABC=80°,∠BCD=50°,利用平移的知识讨论BC与AD+AB的数量关系.

科目:初中数学 来源: 题型:
【题目】如图所示的球形容器上连接着两根导管,容器中盛满了不溶于水的比空气重的某种气体,现在要用向容器中注水的方法来排净里面的气体.水从左导管匀速地注入,气体从右导管排出,那么,容器内剩余气体的体积与注水时间的函数关系的大致图象是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图所示,某公路一侧有A、B两个送奶站,C为公路上一供奶站,CA和CB为供奶路线,现已测得AC=8km,BC=15km,AB=17km,∠1=30°,若有一人从C处出发,沿公路边向右行走,速度为2.5km/h,问:多长时间后这个人距B送奶站最近?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=78°,则∠C的度数为=___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在今年“六一”期间,扬州市某中学计划组织初一学生到上海研学,如果租用甲种客车2辆,乙种客车3辆,则可载180人,如果租用甲种客车3辆,乙种客车1辆,则可载165人.
(1)请问甲、乙两种客车每辆分别能载客多少人?
(2)若该学校初一年级参加研学活动的师生共有303名,旅行社承诺每辆车安排一名导游,导游也需一个座位.旅行前,旅行社的一名导游由于有特殊情况,旅行社只能安排7名导游,为保证所租的每辆车均有一名导游,租车方案调整为:同时租65座、甲种客车和乙种客车的大小三种客车,出发时,所租的三种客车的座位恰好坐满,请问旅行社的租车方案应如何安排?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形以特殊的对称美而深受人们的喜爱,在生产生活中有着广泛的应用,小龙家里有一面长4.2m、宽2.8m的墙壁准备装修,现有如图甲所示的型号瓷砖,其形状是一块长30cm、宽20cm的矩形,中间白色部分为菱形,阴影部分为带淡蓝色花纹的全等的四个直角三角形,解答下列各问:

(1)小龙家里的墙壁最少要贴这种瓷砖多少块?
(2)全部贴满后,这面墙壁上有多少个有淡蓝色花纹的菱形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知四边形ABCD为菱形,且A(0,3)、B(﹣4,0).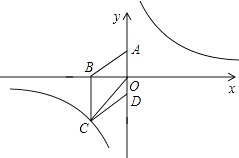
(1)求经过点C的反比例函数的解析式;
(2)设P是(1)中所求函数图象上一点,以P、O、A顶点的三角形的面积与△COD的面积相等.求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
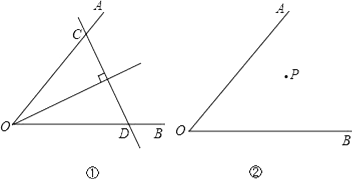
【题目】已知∠AOB及其内部一点P,试讨论以下问题的解答:
(1)如图①,若点P在∠AOB的平分线上,我们可以过P点作直线垂直于角平分线,分别交OA、OB于点C、D,则可以得到△OCD是以CD为底边的等腰三角形;若点P不在∠AOB的平分线上(如图②),你能过P点作直线,分别交OA、OB于点C、D,得到△OCD是等腰三角形,且CD是底边吗?请你在图②中画出图形,并简要说明画法.
(2)若点P不在∠AOB的平分线上(如图③),我们可以过P点作PQ∥OA,并作∠QPR=∠AOB,直线PR分别交OA、OB于点C、D,则可以得到△OCD是以OC为底的等腰三角形.请你说明这样作的理由.
(3)若点P不在∠AOB的平分线上,请你利用在(2)中学到的方法,在图④中过P点作直线分别交OA、OB于点C、D,使得△OCD是等腰三角形,且OD是底边.保留画图的痕迹,不用写出画法.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com