
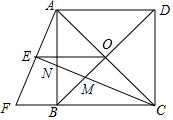
 如图,正方形ABCD的对角线AC、BD相交于点O,延长CB至点F,使CF=CA,∠ACF的平分线分别交AF、AB、BD于点E、N、M,连接EO.
如图,正方形ABCD的对角线AC、BD相交于点O,延长CB至点F,使CF=CA,∠ACF的平分线分别交AF、AB、BD于点E、N、M,连接EO.分析 (1)利用正方形的性质和勾股定理计算即可;
(2)连接FN,根据等腰三角形三线合一的性质证得CE⊥AF,进一步得出∠BAF=∠BCN,然后通过证得△ABF≌△CBN得出BF=BN,进而证得△CFN∽△EOM,根据相似三角形的性质,可得EM与CN的数量关系.
解答 解:(1)∵四边形ABCD是正方形,
∴△ABD是等腰直角三角形,
∴2AB2=BD2,
∵BD=$\sqrt{2}$,
∴AB=1,
∴正方形ABCD的边长为1;
(2)EM=$\frac{1}{2}$CN.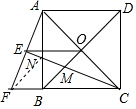 理由如下:
理由如下:
连接FN,
∵CF=CA,CE是∠ACF的平分线,
∴CE⊥AF,
∴∠AEN=∠CBN=90°,
∵∠ANE=∠CNB,
∴∠BAF=∠BCN,
在△ABF和△CBN中,
$\left\{\begin{array}{l}{∠BAF=∠BCN}\\{∠ABF=∠CBN=90°}\\{AB=BC}\end{array}\right.$,
∴△ABF≌△CBN(AAS),
∴BF=BN,
∴∠CBN=∠FNB=45°,
∵四边形ABCD是正方形,
∴∠DBC=45°,
∵EO∥BC,
∴∠EOM=∠DBC=45°,∠OEM=∠FCN,
∴∠CFN=∠EOM,
∴△CFN∽△EOM,
∴$\frac{EM}{CN}=\frac{EO}{CF}$,
即$\frac{EM}{CN}=\frac{\sqrt{2}}{2\sqrt{2}}$.
∴EM=$\frac{1}{2}$CN.
点评 本题考查了正方形的性质,勾股定理的应用,等腰三角形三线合一的性质,三角形全等的判定和性质,三角形相似的判定和性质,熟练掌握性质定理是解题的关键.


科目:初中数学 来源: 题型:填空题
 课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成(4,3).
课间操时,小华、小军、小刚的位置如图,小华对小刚说,如果我的位置用(0,0)表示,小军的位置用(2,1)表示,那么你的位置可以表示成(4,3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
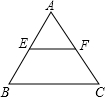 如图所示,刘伯伯家有一块等边三角形的空地,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是( )
如图所示,刘伯伯家有一块等边三角形的空地,已知E,F分别是边AB,AC的中点,量得EF=5米,他想把四边形BCFE用篱笆围起来放养小鸡,则需用篱笆的长是( )| A. | 15米 | B. | 20米 | C. | 25米 | D. | 30米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.
已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com