
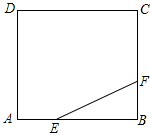
 ��ͼ��������ABCD�ı߳�Ϊ3����E��F�ֱ��ڱ�AB��BC�ϣ�AE=BF=1��С��P�ӵ�E������ֱ�����F�˶���ÿ�����������εı�ʱ����������ʱ����ǵ�������ǣ���С��P��һ������BC��ʱ��С��P��������·��Ϊ$\sqrt{5}$����С��P��һ������AD��ʱ��С��P��������·��Ϊ$\frac{5}{2}\sqrt{5}$����С��P��n��nΪ����������������Fʱ��С��P��������·��Ϊ$6\sqrt{5}n\;-5\sqrt{5}$��
��ͼ��������ABCD�ı߳�Ϊ3����E��F�ֱ��ڱ�AB��BC�ϣ�AE=BF=1��С��P�ӵ�E������ֱ�����F�˶���ÿ�����������εı�ʱ����������ʱ����ǵ�������ǣ���С��P��һ������BC��ʱ��С��P��������·��Ϊ$\sqrt{5}$����С��P��һ������AD��ʱ��С��P��������·��Ϊ$\frac{5}{2}\sqrt{5}$����С��P��n��nΪ����������������Fʱ��С��P��������·��Ϊ$6\sqrt{5}n\;-5\sqrt{5}$�� ���� ������֪�еĵ�E��F��λ�ã���֪����ǵ�����ֵΪ$\frac{1}{2}$��ͨ�����������Σ���ȷ�������ĵ��λ�ã��Ӷ��ɵ÷���Ĵ��������ɹ��ɶ����Ϳ������С����·�����ܳ��ȣ�
��� �⣺������֪�еĵ�E��F��λ�ã���֪����ǵ�����ֵΪ$\frac{1}{2}$����һ����ײ��ΪF���ڷ���Ĺ����У���������ǵ��ڷ���Ǽ�ƽ�й�ϵ�������ε����ƿɵã�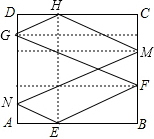
�ڶ�����ײ��ΪG����DA�ϣ���DG=$\frac{1}{6}$DA��
��������ײ��ΪH����DC�ϣ���DH=$\frac{1}{3}$DC��
���Ĵ���ײ��ΪM����CB�ϣ���CM=$\frac{1}{3}$BC��
�������ײ��ΪN����DA�ϣ���AN=$\frac{1}{6}$AD��
�����λص�E�㣬AE=$\frac{1}{3}$AB��
�ɹ��ɶ������Եó�EF=$\sqrt{5}$��FG=$\frac{3}{2}\sqrt{5}$��GH=$\frac{1}{2}\sqrt{5}$��HM=$\sqrt{5}$��MN=$\frac{3}{2}\sqrt{5}$��NE=$\frac{1}{2}\sqrt{5}$��
��С��P��һ������AD��ʱ��С��P��������·��Ϊ$\frac{5}{2}\sqrt{5}$����С��P��n��nΪ����������������Fʱ��С��P��������·��Ϊ6$\sqrt{5}$n-5$\sqrt{5}$��
�ʴ�Ϊ��$\sqrt{5}$��$\frac{5}{2}\sqrt{5}$��6$\sqrt{5}$n-5$\sqrt{5}$��
���� ������Ҫ�����˷���ԭ��������������֪ʶ�����ã�ͨ�����������Σ���ȷ�������ĵ��λ�ã��Ӷ��ɵ÷���Ĵ������ɹ��ɶ�����ȷ��С����·�̣���һ��ѧ���ۺ����⣬�������⣮


 ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
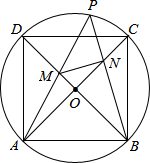 ��ͼ��������ABCD�ڽ��ڡ�O��PΪ�ӻ�$\widehat{CD}$��һ�㣬PA��BD�ڵ�M��PB��AC�ڵ�N���ǡ�PBD=�ȣ���MN��PB����2cos2��-tan�ȵ�ֵ��������
��ͼ��������ABCD�ڽ��ڡ�O��PΪ�ӻ�$\widehat{CD}$��һ�㣬PA��BD�ڵ�M��PB��AC�ڵ�N���ǡ�PBD=�ȣ���MN��PB����2cos2��-tan�ȵ�ֵ��������| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | $\frac{{\sqrt{2}}}{2}$ | D�� | $\frac{{\sqrt{2}}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
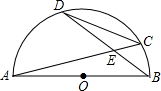 ��ԲO��ֱ��AB=9������AB��CD�ཻ�ڵ�E����CD=$\frac{27}{5}$����BD=7����DE=3$\sqrt{2}$��
��ԲO��ֱ��AB=9������AB��CD�ཻ�ڵ�E����CD=$\frac{27}{5}$����BD=7����DE=3$\sqrt{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
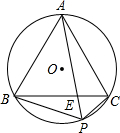 ��ͼ������ABC�ڽ��ڡ�O��P���ӻ�BC������һ�㣬PA��BC���ڵ�E�������½��ۣ�
��ͼ������ABC�ڽ��ڡ�O��P���ӻ�BC������һ�㣬PA��BC���ڵ�E�������½��ۣ�| A�� | 5�� | B�� | 4�� | C�� | 3�� | D�� | 2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
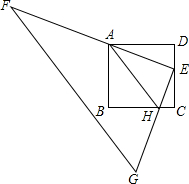 ��ͼ��������ABCD�ı߳�Ϊ4��Rt��FEG��ֱ�Ƕ���E�������εı�DC���˶���һ��ֱ�DZ�EFʼ�վ�����A����һֱ�DZ�EG�������εı�BC�ڵ�H��
��ͼ��������ABCD�ı߳�Ϊ4��Rt��FEG��ֱ�Ƕ���E�������εı�DC���˶���һ��ֱ�DZ�EFʼ�վ�����A����һֱ�DZ�EG�������εı�BC�ڵ�H���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com