
| 1 |
| x2-2x |
| 1 |
| x2-4x+4 |
| 2 |
| x2-2x |
| 1 |
| x2-2x |
| 1 |
| x2-4x+4 |
| 2 |
| x2-2x |
| 1 |
| x(x-2) |
| 1 |
| (x-2)2 |
| 2 |
| x(x-2) |
| 1 |
| x(x-2) |
| 1 |
| (x-2)2 |
| x(x-2) |
| 2 |
| 1 |
| x(x-2) |
| x(x-2) |
| 2 |
| 1 |
| (x-2)2 |
| x(x-2) |
| 2 |
| 1 |
| 2 |
| x |
| 2(x-2) |
| x-2-x |
| 2(x-2) |
| 1 |
| x-2 |
| 1 |
| 2012-2 |
| 1 |
| 2010 |


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
 (2012•瑶海区三模)姚明将带队来我市体育馆进行表演比赛,市体育局在策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).
(2012•瑶海区三模)姚明将带队来我市体育馆进行表演比赛,市体育局在策划本次活动,在与单位协商团购票时推出两种方案.设购买门票数为x(张),总费用为y(元).查看答案和解析>>
科目:初中数学 来源: 题型:
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| a-nx |
| 3 |
| a-nx |
| 3 |
| a |
| 2n |
| a |
| 2n |
| a2 |
| 12n |
| a2 |
| 12n |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
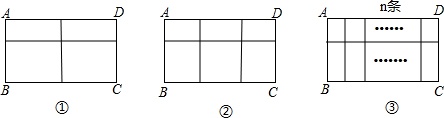
 (2012•道里区三模)小张计划用长为6米的铝合金条制成一个矩形窗架(窗架中的横梁、竖梁皆用铝合金条制作)如图所示.若AB的长为x米,窗户的透光面积为S平方米(铝合金条所占的面积忽略不计).
(2012•道里区三模)小张计划用长为6米的铝合金条制成一个矩形窗架(窗架中的横梁、竖梁皆用铝合金条制作)如图所示.若AB的长为x米,窗户的透光面积为S平方米(铝合金条所占的面积忽略不计).| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•建阳市模拟)小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊到B′处,紧绷着的吊绳A′B′=AB.AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA=
(2012•建阳市模拟)小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊到B′处,紧绷着的吊绳A′B′=AB.AB垂直地面O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA=| 3 |
| 5 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com