
 如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=1:20.
如图,在△ABC中,D、E分别是AB、BC上的点,且DE∥AC,若S△BDE:S△CDE=1:4,则S△BDE:S△ACD=1:20. 分析 根据等高三角形面积的比等于底的比和相似三角形面积的比等于相似比的平方即可解出结果.
解答 解:∵S△BDE:S△DEC=1:4,
∴BE:EC=1:4,
∴BE:BC=1:5,
∵DE∥AC,
∴△BED∽△BCA,
∴$\frac{{S}_{△BED}}{{S}_{△BCA}}$=${(\frac{BE}{BC})}^{2}$=$\frac{1}{25}$,
设S△BED=k,则S△DEC=4k,S△ABC=25k,
∴S△ADC=20k,
∴S△BDE:S△DCA=1:20.
故答案为:1:20.
点评 本题考查了相似三角形的性质,相似三角形面积的比等于相似比的平方,注意各三角形面积之间的关系是解题的关键.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
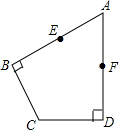 如图,在四边形ABCD中,AB⊥BC,AD⊥CD,AB=AD=6,∠BAD=60°.
如图,在四边形ABCD中,AB⊥BC,AD⊥CD,AB=AD=6,∠BAD=60°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
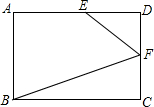 已知:E、F分别是矩形ABCD的边AD、CD上一点,且DF=CF,∠DEF=2∠CBF.若AB=4,BC=6,则AE=$\frac{10}{3}$.
已知:E、F分别是矩形ABCD的边AD、CD上一点,且DF=CF,∠DEF=2∠CBF.若AB=4,BC=6,则AE=$\frac{10}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
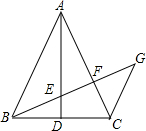 如图所示,在△ABC中,AB=AC,AD⊥BC,CG∥AB,BG分别交AD,AC于E,F.若$\frac{EF}{BE}=\frac{2}{3}$,那么$\frac{GE}{BE}$的值为$\frac{3}{2}$.
如图所示,在△ABC中,AB=AC,AD⊥BC,CG∥AB,BG分别交AD,AC于E,F.若$\frac{EF}{BE}=\frac{2}{3}$,那么$\frac{GE}{BE}$的值为$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
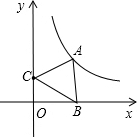 如图,点A是反比例函数y=$\frac{5\sqrt{3}}{x}$(x>0)图象上一点,点B是x轴正半轴上一点,点C的坐标为(0,2),当△ABC是等边三角形时,点A的坐标为($\frac{3\sqrt{3}}{5}$,$\frac{25}{3}$).
如图,点A是反比例函数y=$\frac{5\sqrt{3}}{x}$(x>0)图象上一点,点B是x轴正半轴上一点,点C的坐标为(0,2),当△ABC是等边三角形时,点A的坐标为($\frac{3\sqrt{3}}{5}$,$\frac{25}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com