
分析 题中只说明是等腰三角形没有指明是锐角三角形还是钝角三角形,所以应该分两情况进行分析.
解答 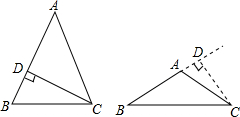 解:①如图,△ABC中,AB=AC,CD⊥AB,
解:①如图,△ABC中,AB=AC,CD⊥AB,
∵△ABC中,CD⊥AB且CD=2$\sqrt{3}$,AB=4,AB=AC,
∴sinA=$\frac{CD}{AC}$=$\frac{2\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$,
∴∠A=60°.
②如图,△ABC中,AB=AC,CD⊥BA的延长线于点D,
∵△ABC中,CD⊥AB且CD=2$\sqrt{3}$,AB=4,AB=AC,
∴sin∠DAC=$\frac{CD}{AC}$=$\frac{2\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$,
∴∠DAC=60°,
∴∠BAC=120°.
故答案为:60°或120°.
点评 本题考查了直角三角形的性质以及等腰三角形的性质,解题时要认真审题,弄清题意是关键,此题难度不大,易于理解.


科目:初中数学 来源: 题型:解答题
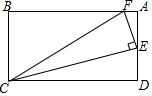 已知,如图,在矩形ABC中.E是AD的中点,EF⊥EC交AB于点F,连FC(AB>AE),求证:$\frac{DE}{AB}$=$\frac{AF}{DE}$.
已知,如图,在矩形ABC中.E是AD的中点,EF⊥EC交AB于点F,连FC(AB>AE),求证:$\frac{DE}{AB}$=$\frac{AF}{DE}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 4 | 6 | 8 | 10 | … | 2n | … |
| 3 | 8 | 15 | 24 | … | … | |
| 5 | 10 | 17 | 26 | … | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com