

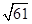 ;
;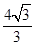 ��
��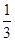 BD��
BD��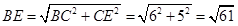 ,
,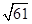 ;
;
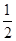 ��ABC=30��,
��ABC=30��,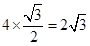 ,
,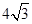 ,
,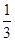 BD=
BD=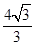 ��
��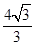 ��
��

 Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д� �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
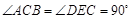 ��
��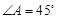 ��
��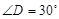 ���
���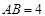 ��
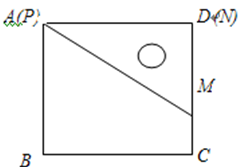
��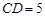 �������ǰ�
�������ǰ� ���ŵ�C˳ʱ����ת
���ŵ�C˳ʱ����ת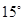 �õ���
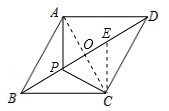
�õ���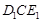 (��ͼ2)����ʱAB��
(��ͼ2)����ʱAB��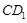 ���ڵ�O�����߶�
���ڵ�O�����߶�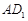 �ij���Ϊ�� ��
�ij����� ��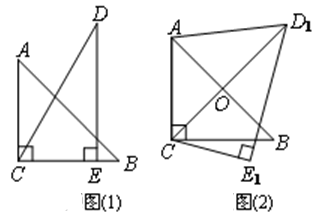
A��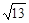 | B��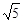 | C��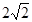 | D��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A���ȱ������� | B��ֱ�������� | C������ | D���������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��C | B��L | C��X | D��Z |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com