
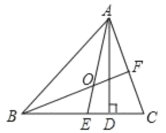
【题目】(1)如图,在![]() 中,
中,![]() 是高,
是高,![]() 是角平分线,它们相交于点
是角平分线,它们相交于点![]() ,
,![]() .求
.求![]() 和
和![]() 的度数.
的度数.
(2)一个多边形的内角和是外角和的3倍,它是几边形?若这个多边形的各个内角都相等,求这个多边形的每个内角的度数.
【答案】(1)![]() =120°,
=120°,![]() =10°;(2)多边形为8边形;每个内角的度数为135°.
=10°;(2)多边形为8边形;每个内角的度数为135°.
【解析】
(1)根据三角形的内角和定理,可求出∠BAC的度数,结合![]() 是角平分线,求出∠EAC的度数,由
是角平分线,求出∠EAC的度数,由![]() 是高,可以依据直角三角形两锐角互余,可求出∠DAC的度数,代入
是高,可以依据直角三角形两锐角互余,可求出∠DAC的度数,代入![]() 中求解;运用角平分线的定义及三角形内角和定理即可求出
中求解;运用角平分线的定义及三角形内角和定理即可求出![]() ;
;
(2)依据多边形内角和公式和外角和为360°,结合已知条件,列出关于边数的方程,解出即可;多边形内角和÷边数即得每个内角的度数.
解:(1)![]() 是
是![]() 的高,
的高,
∴![]() ,
,
∴在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() 、
、![]() 是角平分线,
是角平分线,
![]() ,
,
![]() ,
,
∴![]() =40°-30°=10°,
=40°-30°=10°,
在![]() 中,
中,![]() .
.
答:![]() =120°,
=120°,![]() =10°.
=10°.
(2)设多边形为n边形.
依题意得:(n-2)×180°=3×360°,解之得:n=8,
∴多边形为8边形,
若这个多边形的各个内角都相等,
则每个内角的度数=3×360°÷8=135°.
答:多边形为8边形;每个内角的度数为135°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
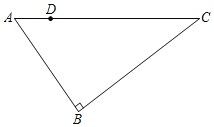
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点D为AC边上的个动点,点D从点A出发,沿边AC向C运动,当运动到点C时停止,设点D运动时间为t秒,点D运动的速度为每秒1个单位长度的.
(1)当t=2时,求CD的长;
(2)求当t为何值时,线段BD最短?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象的对称轴是直线![]() ,它与
,它与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交与点
轴交与点![]() ,点
,点![]() 、
、![]() 的坐标分别是
的坐标分别是![]() 、
、![]() .
.

(1)请在平面直角坐标系内画出示意图;
(2)求此图象所对应的函数关系式;
(3)若点![]() 是此二次函数图象上位于
是此二次函数图象上位于![]() 轴上方的一个动点,求
轴上方的一个动点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
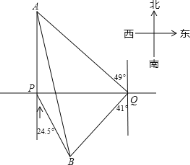
【题目】一轮船在![]() 处测得灯塔
处测得灯塔![]() 在正北方向,灯塔
在正北方向,灯塔![]() 在南偏东
在南偏东![]() 方向,轮船向正东航行了
方向,轮船向正东航行了![]() ,到达
,到达![]() 处,测得
处,测得![]() 位于北偏西
位于北偏西![]() 方向,
方向,![]() 位于南偏西
位于南偏西![]() 方向.
方向.
(1)线段![]() 与
与![]() 是否相等?请说明理由;
是否相等?请说明理由;
(2)求![]() 、
、![]() 间的距离(参考数据
间的距离(参考数据![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
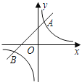
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当![]() 取何值时,反比例函数的值大于一次函数的值.
取何值时,反比例函数的值大于一次函数的值.
(3)求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
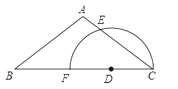
【题目】已知:如图,在△ABC中,D是边BC上一点,以点D为圆心,CD为半径作半圆,分别与边AC、BC相交于点E和点F.如果AB=AC=5,cosB=![]() ,AE=1.求:
,AE=1.求:
(1)线段CD的长度;
(2)点A和点F之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2, 求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com