
【题目】直线 AB∥CD,直线 a 分别交 AB、CD 于点 E、F,点 M 在线段 EF 上,点 P 是 直线 CD 上的一个动点(点 P 不与点 F 重合).
(1)如图 1,当点 P 在射线 FC 上移动时,∠FMP+∠FPM 与∠AEF 有什么数量关系? 请说明理由;
(2)如图 2,当点 P 在射线 FD 上移动时,∠FMP+∠FPM 与∠AEF 有什么数量关系? 请说明理由.

【答案】(1)∠AEF=∠MPF+∠FPM;(2)∠FMP+∠FPM+∠AEF=180°;
【解析】
(1)由AB∥CD,利用两直线平行,同旁内角互补,可得∠AEF十∠EFC=180°,又由三角形内角和定理,即可得∠FMP+∠FPM+∠EFC=180°,则可得∠FMP+∠FPM=∠AEF;
(2)由AB∥CD,利用两直线平行,内错角相等,即可证得∠AEF=∠EFD,又由三角形内角和定理,即可得∠FMP+∠FPM+∠EFD=180°,则可得∠FMP+∠FPM+∠AEF=180°.
(1)∠FMP+∠FPM=∠AEF,
理由:∵AB∥CD,
∴∠AEF=∠DFM,
又∵∠FMP+∠FPM=∠DFM,
∴∠FMP+∠FPM=∠AEF;
(2)∠FMP+∠FPM与∠AEF互补(或∠FMP+∠FPM+∠AEF=180)…(8分)
理由:∵AB∥CD,
∴∠AEF=∠EFD(两直线平行,内错角相等),
∵∠FMP+∠FPM+∠EFD=180(三角形内角和定理),
∴∠FMP+∠FPM+∠AEF=180(等量代换).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD//BC,BD=BC,∠ABC=900;

(1)画出![]() 的高CE;;
的高CE;;
(2)请写出图中的一对全等三角形(不添加任何字母),并说明理由;
(3)若![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开设了丰富多彩的实践类拓展课程,分别设置了体育类、艺术类、文学类及其它类课程(要求人人参与,每人只能选择一门课程).为了解学生喜爱的拓展课类别,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:

(1)此次共调查了多少人?
(2)请将条形统计图补充完整
(3)求文学类课程在扇形统计图中所占圆心角的度数;
(4)若该校有1500名学生,请估计喜欢体育类拓展课的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() 平分
平分![]() (
(![]() ),
),![]() 为
为![]() 上一点,且
上一点,且![]() 于点
于点![]() .
.
(1)当![]() ,
,![]() 时,求
时,求![]() 的度数;
的度数;
(2)若![]() ,
,![]() ,请结合(1)的计算猜想
,请结合(1)的计算猜想![]() 、
、![]() 、
、![]() 之间的数量关系,直接写出答案,不说明理由;(用含有
之间的数量关系,直接写出答案,不说明理由;(用含有![]() 、
、![]() 的式子表示
的式子表示![]() )
)
(3)如图②,当点![]() 在
在![]() 的延长线上时,其余条件不变,则(2)中的结论还成立吗?若成立,请说明为什么;若不成立,请写出成立的结论,并说明为什么.
的延长线上时,其余条件不变,则(2)中的结论还成立吗?若成立,请说明为什么;若不成立,请写出成立的结论,并说明为什么.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD中,点E在边DC上,DE=2,EC=1(如图所示)把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为______.
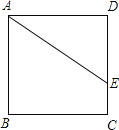
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将□ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
⑴求证:△ABF≌△ECF;⑵若∠AFC=2∠D,连接AC、BE.求证:四边形ABEC是矩形.
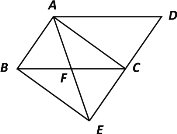
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD对折,使它落在斜边AB上,且与AE重合,则CD等于( )
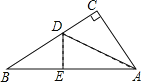
A. 3cmB. 4cmC. 5cmD. 6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 和△BDE 都是等边三角形,A、B、D 三点共线.下列结论:①AB=CD;②BF=BG;③HB 平分∠AHD;④∠AHC=60°,⑤△BFG 是等边三角形.其中正确的有____________(只填序号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com