
°æƒø°ø»ÁÕº1£¨≈◊ŒÔœfly£Ωax2+bx+cµƒ∂•µ„£®0£¨5£©£¨«“π˝µ„£®©Å3£¨![]() £©£¨œ»«Û≈◊ŒÔœflµƒΩ‚Œˆ Ω£¨‘ŸΩ‚戜¬¡–Œ £∫
£©£¨œ»«Û≈◊ŒÔœflµƒΩ‚Œˆ Ω£¨‘ŸΩ‚戜¬¡–Œ £∫
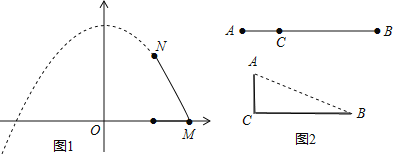
£®”¶”√£©Œ Â1£¨»ÁÕº2£¨œfl∂ŒAB£Ωd£®∂®÷µ£©£¨Ω´∆‰Õ‰’€≥…ª•œ‡¥π÷±µƒ¡Ω∂ŒAC°¢CB∫Û£¨…ËA°¢B¡Ωµ„µƒæ‡¿ÎŒ™x£¨”…A°¢B°¢C»˝µ„◊È≥…Õº–Œ√ʪ˝Œ™S£¨«“S”Îxµƒ∫Ø ˝πÿœµ»ÁÕºÀ˘ 森≈◊ŒÔœfly£Ωax2+bx+c…œMN÷ƺ‰µƒ≤ø∑÷£¨M‘⁄x÷·…œ£©£∫
£®1£©ÃÓø’£∫œfl∂ŒABµƒ≥§∂»d£Ω°° °°£ªÕ‰’€∫ÛA°¢B¡Ωµ„µƒæ‡¿Îxµƒ»°÷µ∑∂Œß «°° °°£ª»ÙS£Ω3£¨‘Ú «∑ҥʑ⁄µ„C£¨Ω´AB∑÷≥…¡Ω∂Œ£®ÃÓ°∞ƒ‹°±ªÚ°∞≤ªƒ‹°±£©°° °°£ª»Ù√ʪ˝S£Ω1.5 ±£¨µ„CΩ´œfl∂ŒAB∑÷≥…¡Ω∂Œµƒ≥§∑÷± «°° °°£ª
£®2£©ÃÓø’£∫‘⁄»ÁÕº1÷–£¨“‘‘≠µ„OŒ™‘≤–ƒ£¨A°¢B¡Ωµ„µƒæ‡¿ÎxŒ™∞Îæ∂µƒ°—O£ªª≠≥ˆµ„C∑÷ABÀ˘µ√¡Ω∂ŒAC”ÎCBµƒ∫Ø ˝ÕºœÛ£®œfl∂Œ£©£ª…Ë‘≤–ƒOµΩ∏√∫Ø ˝ÕºœÛµƒæ‡¿ÎŒ™h£¨‘Úh£Ω°° °°£¨∏√∫Ø ˝ÕºœÛ”ΰ—OµƒŒª÷√πÿœµ «°° °°£Æ
£®Ã·…˝£©Œ Â2£¨“ª∏ˆ÷±Ω«»˝Ω«–Œ–±±fl≥§Œ™c£®∂®÷µ£©£¨…Ë∆‰√ʪ˝Œ™S£¨÷‹≥§Œ™x£¨÷§√˜S «xµƒ∂˛¥Œ∫Ø ˝£¨«Û∏√∫Ø ˝πÿœµ Ω£¨≤¢«Ûxµƒ»°÷µ∑∂Œß∫Õœ‡”¶Sµƒ»°÷µ∑∂Œß£Æ
°æ¥∞∏°ø≈◊ŒÔœflµƒΩ‚Œˆ ΩŒ™£∫y£Ω©Å![]() x2+5£ª£®1£©2
x2+5£ª£®1£©2![]() 0£ºx£º2
0£ºx£º2![]() £¨≤ªƒ‹£¨
£¨≤ªƒ‹£¨![]() +
+![]() ∫Õ
∫Õ![]() ©Å
©Å![]() £ª£®2£©
£ª£®2£©![]() £¨œ‡¿ÎªÚœ‡«–ªÚœ‡Ωª£ª£®3£©œ‡”¶Sµƒ»°÷µ∑∂ŒßŒ™S£æ
£¨œ‡¿ÎªÚœ‡«–ªÚœ‡Ωª£ª£®3£©œ‡”¶Sµƒ»°÷µ∑∂ŒßŒ™S£æ![]() c2£Æ
c2£Æ
°æΩ‚Œˆ°ø
Ω´∂•µ„£®0£¨5£©º∞µ„£®©Å3£¨![]() £©¥˙»Î≈◊ŒÔœflµƒ∂•µ„ Ωº¥ø…«Û≥ˆ∆‰Ω‚Œˆ Ω£ª
£©¥˙»Î≈◊ŒÔœflµƒ∂•µ„ Ωº¥ø…«Û≥ˆ∆‰Ω‚Œˆ Ω£ª
£®1£©”…≈◊ŒÔœflµƒΩ‚Œˆ Ωœ»«Û≥ˆµ„Mµƒ◊¯±Í£¨”…∂˛¥Œ∫Ø ˝µƒÕºœÛº∞–‘÷ º¥ø…≈–∂œdµƒ÷µ£¨ø…”…dµƒ÷µ≈–∂œ≥ˆxµƒ»°÷µ∑∂Œß£¨∑÷±Ω´S£Ω3∫Õ1£Æ5¥˙»Î≈◊ŒÔœflΩ‚Œˆ Ω£¨º¥ø…«Û≥ˆµ„CΩ´œfl∂ŒAB∑÷≥…¡Ω∂Œµƒ≥§£ª
£®2£©…ËAC£Ωy£¨CB£Ωx£¨ø…÷±Ω”–¥≥ˆµ„C∑÷ABÀ˘µ√¡Ω∂ŒAC”ÎCBµƒ∫Ø ˝Ω‚Œˆ Ω£¨≤¢ª≠≥ˆÕºœÛ£¨÷§°˜OPMŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨π˝µ„O◊˜OH°ÕPM”⁄µ„H£¨‘ÚOH£Ω![]() PM£Ω
PM£Ω![]() £¨∑÷«Èøˆø…Ã÷¬€≥ˆAC”ÎCBµƒ∫Ø ˝ÕºœÛ£®œfl∂ŒPM£©”ΰ—OµƒŒª÷√πÿœµ£ª
£¨∑÷«Èøˆø…Ã÷¬€≥ˆAC”ÎCBµƒ∫Ø ˝ÕºœÛ£®œfl∂ŒPM£©”ΰ—OµƒŒª÷√πÿœµ£ª
£®3£©…Ë÷±Ω«»˝Ω«–Œµƒ¡Ω÷±Ω«±fl≥§∑÷±Œ™a£¨b£¨”…π¥π…∂®¿Ìº∞ÕÍ»´∆Ωπ´ Ωø…“‘÷§√˜S «xµƒ∂˛¥Œ∫Ø ˝£¨≤¢ø…–¥≥ˆxµƒ»°÷µ∑∂Œßº∞œ‡”¶Sµƒ»°÷µ∑∂Œß£Æ
Ω‚£∫°fl≈◊ŒÔœfly£Ωax2+bx+cµƒ∂•µ„£®0£¨5£©£¨
°‡y£Ωax2+5£¨
Ω´µ„£®©Å3£¨![]() £©¥˙»Î£¨
£©¥˙»Î£¨
µ√![]() £Ωa°¡£®©Å3£©2+5£¨
£Ωa°¡£®©Å3£©2+5£¨
°‡a£Ω![]() £¨
£¨
°‡≈◊ŒÔœflµƒΩ‚Œˆ ΩŒ™£∫y£Ω![]() £ª
£ª
£®1£©°flS”Îxµƒ∫Ø ˝πÿœµ»ÁÕºÀ˘ 森≈◊ŒÔœfly£Ωax2+bx+c…œMN÷ƺ‰µƒ≤ø∑÷£¨M‘⁄x÷·…œ£©£¨
‘⁄y£Ω![]() £¨µ±y£Ω0 ±£¨x1£Ω2
£¨µ±y£Ω0 ±£¨x1£Ω2![]() £¨x2£Ω©Å2
£¨x2£Ω©Å2![]() £¨
£¨
°‡M£®2![]() £¨0£©£¨
£¨0£©£¨
º¥µ±x£Ω2![]() ±£¨S£Ω0£¨
±£¨S£Ω0£¨
°‡dµƒ÷µŒ™2![]() £ª
£ª
°‡Õ‰’€∫ÛA°¢B¡Ωµ„µƒæ‡¿Îxµƒ»°÷µ∑∂Œß «0£ºx£º2![]() £ª
£ª
µ±S£Ω3 ±£¨…ËAC£Ωa£¨‘ÚBC£Ω2![]() ©Åa£¨
©Åa£¨
°‡![]() a£®2
a£®2![]() ©Åa£©£Ω3£¨
©Åa£©£Ω3£¨
’˚¿Ì£¨µ√a2©Å2![]() a+6£Ω0£¨
a+6£Ω0£¨
°fl°˜£Ωb2©Å4ac£Ω©Å4£º0£¨
°‡∑Ω≥ÃŒfi µ ˝∏˘£ª
µ±S£Ω1.5 ±£¨…ËAC£Ωa£¨‘ÚBC£Ω2![]() ©Åa£¨
©Åa£¨
°‡![]() a£®2
a£®2![]() ©Åa£©£Ω1.5£¨
©Åa£©£Ω1.5£¨
’˚¿Ì£¨µ√a2©Å2![]() a+3£Ω0£¨
a+3£Ω0£¨
Ω‚µ√![]()
![]() £¨
£¨
°‡µ±a£Ω![]() ±£¨2
±£¨2![]() ©Åa£Ω
©Åa£Ω![]() £¨
£¨
µ±a£Ω![]() ±£¨2
±£¨2![]() ©Åa£Ω
©Åa£Ω![]() £¨
£¨
°‡»Ù√ʪ˝S£Ω1.5 ±£¨µ„CΩ´œfl∂ŒAB∑÷≥…¡Ω∂Œµƒ≥§∑÷± «![]() ∫Õ
∫Õ![]() £ª
£ª
π ¥∞∏Œ™£∫2![]() £¨0£ºx£º2
£¨0£ºx£º2![]() £¨≤ªƒ‹£¨
£¨≤ªƒ‹£¨![]() ∫Õ
∫Õ![]() £ª
£ª
£®2£©…ËAC£Ωy£¨CB£Ωx£¨
‘Úy£Ω©Åx+2![]() £¨»ÁÕº1À˘ 浃œfl∂ŒPM£¨
£¨»ÁÕº1À˘ 浃œfl∂ŒPM£¨
‘ÚP£®0£¨2![]() £©£¨M£®2
£©£¨M£®2![]() £¨0£©£¨
£¨0£©£¨
°‡°˜OPMŒ™µ»—¸÷±Ω«»˝Ω«–Œ£¨
°‡PM£Ω![]() OP£Ω2
OP£Ω2![]() £¨
£¨
π˝µ„O◊˜OH°ÕPM”⁄µ„H£¨
‘ÚOH£Ω![]() PM£Ω
PM£Ω![]() £¨
£¨
°‡µ±0£ºx£º![]() ±£¨AC”ÎCBµƒ∫Ø ˝ÕºœÛ£®œfl∂ŒPM£©”ΰ—Oœ‡¿Î£ª
±£¨AC”ÎCBµƒ∫Ø ˝ÕºœÛ£®œfl∂ŒPM£©”ΰ—Oœ‡¿Î£ª
µ±x£Ω![]() ±£¨AC”ÎCBµƒ∫Ø ˝ÕºœÛ£®œfl∂ŒPM£©”ΰ—Oœ‡«–£ª
±£¨AC”ÎCBµƒ∫Ø ˝ÕºœÛ£®œfl∂ŒPM£©”ΰ—Oœ‡«–£ª
µ±![]() £ºx£º2
£ºx£º2![]() ±£¨AC”ÎCBµƒ∫Ø ˝ÕºœÛ£®œfl∂ŒPM£©”ΰ—Oœ‡Ωª£ª
±£¨AC”ÎCBµƒ∫Ø ˝ÕºœÛ£®œfl∂ŒPM£©”ΰ—Oœ‡Ωª£ª
π ¥∞∏Œ™£∫![]() £¨œ‡¿ÎªÚœ‡«–ªÚœ‡Ωª£ª
£¨œ‡¿ÎªÚœ‡«–ªÚœ‡Ωª£ª
£®3£©…Ë÷±Ω«»˝Ω«–Œµƒ¡Ω÷±Ω«±fl≥§∑÷±Œ™a£¨b£¨
‘Ú![]() £¨
£¨
°fl£®a+b£©2£Ωa2+b2+2ab£¨
°‡£®x©Åc£©2£Ωc2+2ab£¨
°‡![]() £¨
£¨
º¥S£Ω![]() £¨
£¨
°‡xµƒ»°÷µ∑∂ŒßŒ™£∫x£æc£¨
‘Úœ‡”¶Sµƒ»°÷µ∑∂ŒßŒ™S£æ![]() £Æ
£Æ



| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
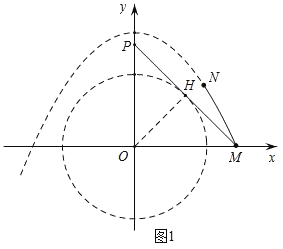
°æƒø°ø»ÁÕº£¨‘⁄»ÒΩ«°˜ABC÷–£¨BC£Ω10£¨AC£Ω11£¨°˜ABCµƒ√ʪ˝Œ™33£¨µ„P «…‰œflCA…œ“ª∂ص„£¨“‘BPŒ™÷±æ∂◊˜‘≤Ωªœfl∂ŒAC”⁄µ„E£¨Ωª…‰œflBA”⁄µ„D£¨Ωª…‰œflCB”⁄µ„F£Æ
£®1£©µ±µ„P‘⁄œfl∂ŒAC…œ ±£¨»Ùµ„EŒ™![]() ÷–µ„£¨«ÛBPµƒ≥§£Æ
÷–µ„£¨«ÛBPµƒ≥§£Æ
£®2£©¡¨Ω·EF£¨»Ù°˜CEFŒ™µ»—¸»˝Ω«–Œ£¨«ÛÀ˘”–¬˙◊„Ãıº˛µƒBP÷µ£Æ
£®3£©Ω´DE»∆µ„DÀ≥ ±’Ζ˝◊™90°„£¨µ±µ„Eµƒ∂‘”¶µ„E'«°∫√¬‰‘⁄BC…œ ±£¨º«°˜DBE'µƒ√ʪ˝Œ™S1£¨°˜DPEµƒ√ʪ˝S2£¨‘Ú![]() µƒ÷µŒ™°° °°£Æ£®÷±Ω”–¥≥ˆ¥∞∏º¥ø…£©
µƒ÷µŒ™°° °°£Æ£®÷±Ω”–¥≥ˆ¥∞∏º¥ø…£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
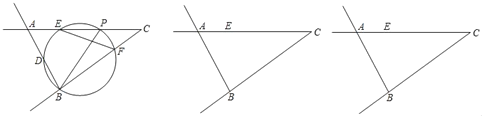
°æƒø°ø»ÁÕº£¨‘⁄…»–ŒOMN÷–£¨°œMON£Ω90°„£¨OM£Ω6£¨°˜ABC «…»–Œµƒƒ⁄Ω”»˝Ω«–Œ£¨∆‰÷–A°¢C°¢B∑÷±‘⁄∞Îæ∂OM°¢ON∫Õª°MN…œ£¨°œACB£Ω90°„£¨BC£∫AC£Ω3£∫8£¨‘Úœfl∂ŒBCµƒ◊Ó–°÷µŒ™_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
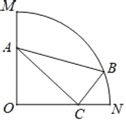
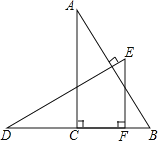
°æƒø°ø»ÁÕº£¨°˜ABC∫Õ°˜DEF∂º «÷±Ω«»˝Ω«–Œ£¨°œACB£Ω°œDFE£Ω90°„£¨AB£ΩDE£¨∂•µ„F‘⁄BC…œ£¨±flDFæ≠π˝µ„C£¨µ„A£¨E‘⁄BCÕ¨≤‡£¨DE°ÕAB£Æ
£®1£©«Û÷§£∫°˜ABC°’°˜DEF£ª
£®2£©»ÙAC£Ω11£¨EF£Ω6£¨CF£Ω4£¨«ÛBDµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨Àƒ±fl–ŒABCD «æÿ–Œ£¨EŒ™CD±fl…œ“ªµ„£¨«“AE°¢BE∑÷±∆Ω∑÷°œDAB°¢°œABC£Æ
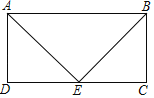
£®1£©«Û÷§£∫°˜ADE°’°˜BCE£ª
£®2£©“—÷™AD£Ω3£¨«Ûæÿ–Œµƒ¡Ì“ª±flABµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄æÿ–ŒABCD÷–£¨AB£Ω16cm£¨BC£Ω6cm£¨µ„P¥”µ„A≥ˆ∑¢—ÿAB“‘3cm/sµƒÀŸ∂»œÚµ„B“∆∂Ø£®≤ª”ε„A£¨B÷ÿ∫œ£©£ªÕ¨ ±µ„Q¥”µ„C≥ˆ∑¢—ÿCD“‘2cm/sµƒÀŸ∂»œÚµ„D“∆∂Ø£®≤ª”ε„C°¢D÷ÿ∫œ£©£¨æ≠π˝º∏√Σ¨°˜PDQŒ™÷±Ω«»˝Ω«–Œ£øÀµ√˜¿Ì”…£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº◊°¢““¡Ω≥µ∑÷±¥”A°¢B¡ΩµÿÕ¨ ±≥ˆ∑¢£¨‘⁄Õ¨“ªÃıπ´¬∑…œ£¨‘»ÀŸ–– ª£¨œ‡œÚ∂¯––£¨µΩ¡Ω≥µœ‡”ˆ ±Õ£÷π.º◊≥µ–– ª“ª∂Œ ±º‰∫Û£¨“Úπ Õ£≥µ0.5–° ±£¨π ’œΩ‚≥˝∫Û£¨ºÃ–¯“‘‘≠ÀŸœÚBµÿ–– ª£¨¡Ω≥µ÷ƺ‰µƒ¬∑≥Ãy£®«ß√◊£©”Î≥ˆ∑¢∫ÛÀ˘”√ ±º‰x(–° ±£©÷ƺ‰µƒ∫Ø ˝πÿœµ»ÁÕºÀ˘ æ.

£®1£©«Ûº◊°¢““¡Ω≥µ–– ªµƒÀŸ∂»Vº◊°¢V““.
£®2£©«Ûmµƒ÷µ.
£®3£©»Ùº◊≥µ√ª”–π ’œÕ£≥µ£¨«Ûø…“‘÷«∞∂‡≥§ ±º‰¡Ω≥µœ‡”ˆ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
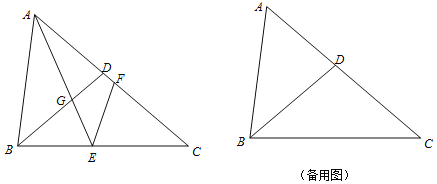
°æƒø°ø»ÁÕº£¨“—÷™°˜ABC÷–£¨AB£Ω8£¨BC£Ω10£¨AC£Ω12£¨D «AC±fl…œ“ªµ„£¨«“AB2£ΩADAC£¨¡¨Ω”BD£¨µ„E°¢F∑÷± «BC°¢AC…œ¡Ωµ„£®µ„E≤ª”ÎB°¢C÷ÿ∫œ£©£¨°œAEF£Ω°œC£¨AE”ÎBDœ‡Ωª”⁄µ„G£Æ
£®1£©«ÛBDµƒ≥§£ª
£®2£©«Û÷§°˜BGE°◊°˜CEF£ª
£®3£©¡¨Ω”FG£¨µ±°˜GEF «µ»—¸»˝Ω«–Œ ±£¨÷±Ω”–¥≥ˆBEµƒÀ˘”–ø…ƒ‹µƒ≥§∂»£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨≈◊ŒÔœfly=x2+£®k©Å1£©x©Åk”Î÷±œfly=kx+1Ωª”⁄A£¨B¡Ωµ„£¨µ„A‘⁄µ„Bµƒ◊Û≤‡£Æ

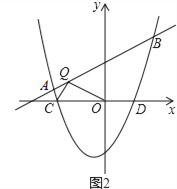
£®1£©»ÁÕº1£¨µ±k=1 ±£¨÷±Ω”–¥≥ˆA£¨B¡Ωµ„µƒ◊¯±Í£ª
£®2£©‘⁄£®1£©µƒÃıº˛œ¬£¨µ„PŒ™≈◊ŒÔœfl…œµƒ“ª∏ˆ∂ص„£¨«“‘⁄÷±œflABœ¬∑Ω£¨ ‘«Û≥ˆ°˜ABP√ʪ˝µƒ◊Ó¥Û÷µº∞¥À ±µ„Pµƒ◊¯±Í£ª
£®3£©»ÁÕº2£¨≈◊ŒÔœfly=x2+£®k©Å1£©x©Åk£®k£æ0£©”Îx÷·Ωª”⁄µ„C°¢D¡Ωµ„£®µ„C‘⁄µ„Dµƒ◊Û≤‡£©£¨‘⁄÷±œfly=kx+1…œ «∑ҥʑ⁄Œ®“ª“ªµ„Q£¨ πµ√°œOQC=90°„£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆ¥À ±kµƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com