
【题目】如图,在矩形ABCD中,已知AB=2 ![]() ,AD=2,点P是对角线BD上一动点(不与B,D重合),连接AP,过点P作PE⊥AP,交DC于点E,
,AD=2,点P是对角线BD上一动点(不与B,D重合),连接AP,过点P作PE⊥AP,交DC于点E,
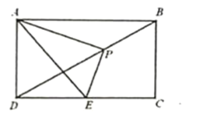
(1)求证:∠PAD=∠PEC;
(2)当点P是BD的中点时,求DE的值;
(3)在点P运动过程中,当DE= ![]() 时,求BP的值.
时,求BP的值.
【答案】(1)见解析;(2)![]() (3)
(3)![]()
【解析】
(1)利用四边形的内角和和三角形外角的性质得∠DEP+∠DAP=180°,∠DEP+∠PEC=180°,再利用同角的补角相等可得结论;
(2)连接AC,交BD于P.先利用特殊角的三角函数值求出∠ADB=60°,再利用对角线的性质可得PA=PD,故△ADP为等边三角形,则AP=AD=2;然后易证Rt△ADE≌Rt△APE,可得∠DAE=∠PAE=30°,进而在Rt△ADE中利用tan∠DAE的正切求解即可;
(3)作PG⊥AB于G,GP的延长线交DC于H,得四边形ADGH是矩形,PG⊥DC,则GH=BC=2;设PG=a,则PH=GH﹣PH=2﹣a,在Rt△BGP中利用tan∠PBG表示出BG和AG;然后易证△AGP∽△PHE,利用相似三角形的对应边成比例列出关于a比例方程并求解,即可利用BP=2PG=2a计算即可.
解:(1)证明:∵PE⊥AP,
∴∠APE=90°,
∵四边形ABCD是矩形,
∴∠ADC=90°,
在四边形ADEP中∠ADE+∠DEP+∠APE+∠DAP=360°,
∴∠DEP+∠DAP=360°-90°-90°=180°,
又∵∠DEP+∠PEC=180°,
∴∠PAD=∠PEC;
(2)解:∵四边形ABCD是矩形,AB=![]() ,AD=2,
,AD=2,
∴![]() ,
,
∴∠BDA=60°,
连接AC,
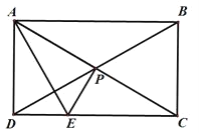
∵点P是BD的中点,
∴点P为AC与BD的交点,
∴△ADP为等边三角形,
∴AP=AD=2,
在Rt△ADE和Rt△APE中![]() ,
,
∴Rt△ADE≌Rt△APE(HL),
∴∠DAE=∠PAE=30°,
∴![]() ,
,
∴ ![]() ;
;
(3)解:如图,过点P作PG⊥AB于G,GP的延长线交DC于H,四边形ABCD是矩形,
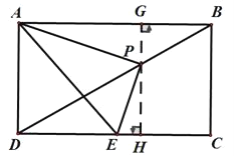
∴PG⊥DC,
∴GH=BC=2,
设PG=a,则PH=GH﹣PH=2﹣a,
在Rt△BGP中,tan∠PBG=![]() ,
,
∴BG=![]() PG=
PG=![]() a,
a,
∴AG=AB-BG=2![]() -
-![]() a=
a=![]() (2-a),
(2-a),
EH=DH-DE=2![]() -
-![]() a-
a-![]() =
=![]() -
-![]() a,
a,
∵PG⊥DC,
∴∠APG+∠EPH=90°,
∵∠APG+∠PAG=90°,
∴∠EPH=∠PAG,
∵∠AGP=∠PHE=90°,
∴△AGP∽△PHE,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴BP=2PG=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.
(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 ;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太阳能光伏发电因其清洁、安全、便利、高效等特点,已成为世界各国普遍关注和重点发展的新兴产业,如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,均为300cm,AB的倾斜角为![]() ,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,
,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,![]() 于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30cm,点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少cm(结果保留根号)
于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为30cm,点A到地面的垂直距离为50cm,求支撑角钢CD和EF的长度各是多少cm(结果保留根号)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y1=ax2+bx+c(a≠0)图象的一部分,抛物线的顶点坐标A(1,3),与x轴的一个交点B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论: ①2a+b=0;②abc>0;③方程ax2+bx+c=3有两个相等的实数根;④抛物线与x轴的另一个交点是(﹣1,0);⑤当1<x<4时,有y2<y1 ,
其中正确的是________.
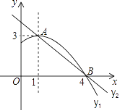
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解朝阳社区![]() 岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
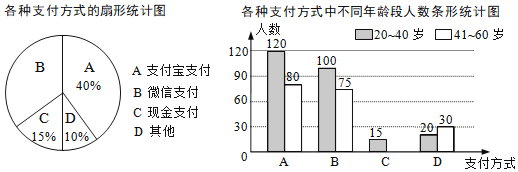
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中![]() 岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
岁的居民约8000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=![]() x2+
x2+![]() x+3与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,过点C作x轴的平行线交抛物线于点P.连接AC.
x+3与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,过点C作x轴的平行线交抛物线于点P.连接AC.
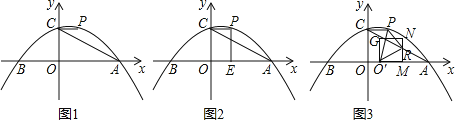
(1)求点P的坐标及直线AC的解析式;
(2)如图2,过点P作x轴的垂线,垂足为E,将线段OE绕点O逆时针旋转得到OF,旋转角为α(0°<α<90°),连接FA、FC.求AF+![]() CF的最小值;
CF的最小值;
(3)如图3,点M为线段OA上一点,以OM为边在第一象限内作正方形OMNG,当正方形OMNG的顶点N恰好落在线段AC上时,将正方形OMNG沿x轴向右平移,记平移中的正方形OMNG为正方形O′MNG,当点M与点A重合时停止平移.设平移的距离为t,正方形O′MNG的边MN与AC交于点R,连接O′P、O′R、PR,是否存在t的值,使△O′PR为直角三角形?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
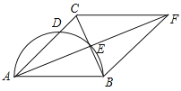
【题目】如图,在△ABC中,AB=AC,以AB为直径的半圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB、FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=![]() ,BE=1,求半圆的面积.
,BE=1,求半圆的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着社会经济的发展,汽车逐渐走入平常百姓家.某数学兴趣小组随机抽取了我市某单位部分职工进行调查,对职工购车情况分4类(A:车价40万元以上;B:车价在20—40万元;C:车价在20万元以下;D:暂时未购车)进行了统计,并将统计结果绘制成以下条形统计图和扇形统计图.请结合图中信息解答下列问题:
(1)调查样本人数为__________,样本中B类人数百分比是_______,其所在扇形统计图中的圆心角度数是________;
(2)把条形统计图补充完整;
(3)该单位甲、乙两个科室中未购车人数分别为2人和3人,现从中选2人去参观车展,用列表或画树状图的方法,求选出的2人来自不同科室的概率.
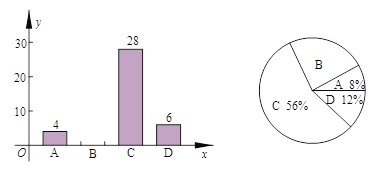
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com