
 (2013•南昌模拟)已知抛物线m:y=ax2-2ax+a-1,顶点为A,将抛物线m绕着点(-1,0)旋转180°后得到抛物线n,顶点为C.
(2013•南昌模拟)已知抛物线m:y=ax2-2ax+a-1,顶点为A,将抛物线m绕着点(-1,0)旋转180°后得到抛物线n,顶点为C.| p+q |
| 2 |
| 3 |
| 16 |
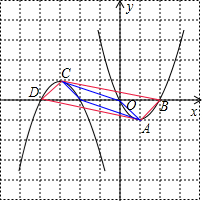 (2)如图,设B点坐标为(p,p2-2p),D(q,-q2-6q-8),
(2)如图,设B点坐标为(p,p2-2p),D(q,-q2-6q-8),| p+q |
| 2 |
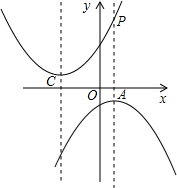
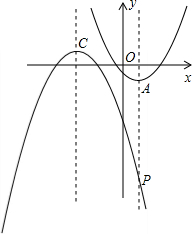 (3)①如图,设抛物线n的解析式为y=-a(x+3)2+1,
(3)①如图,设抛物线n的解析式为y=-a(x+3)2+1,| 1 |
| 2 |
| 1 |
| 4 |
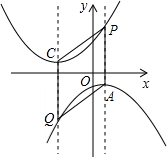 ∵抛物线n的对称轴为直线x=-3,
∵抛物线n的对称轴为直线x=-3,| 3 |
| 16 |
| 3 |
| 16 |


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
 (2013•南昌模拟)均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),则这个容器的形状为( )
(2013•南昌模拟)均匀地向一个容器注水,最后把容器注满.在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为一折线),则这个容器的形状为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com