
����Ŀ��ABCD�У��Խ���AC��BD�ཻ�ڵ�O��E�DZ�AB�ϵ�һ�����㣨����A��B�غϣ�������EO���ӳ�����CD�ڵ�F������AF��CE�������ĸ������У�
�ٶ��ڶ���E���ı���AECFʼ����ƽ���ı��Σ�
������ABC��90���������ٴ���һ����E��ʹ���ı���AECF�Ǿ��Σ�
����AB��AD�������ٴ���һ����E��ʹ���ı���AECF�����Σ�
������BAC��45���������ٴ���һ����E��ʹ���ı���AECF�������Σ�
����������ȷ˵���������_____��
���𰸡��٢ۢ�
��������
�ٸ���ƽ���ı��ε����ʵ�AB��DC��OA��OC������ƽ���ߵ����ʺͶԶ�����ȿɵá�OAE����OCF����AOE����COF������ASA���ж���AOE�ա�COF���Ƴ�AE=CF,�ɴ˿��ж��ı���Ϊƽ���ı��Σ�
�ڸ��ݾ��ε��ж�������֪����CE��ABʱ���ı���AECFΪ���Σ���ͼ2-2�У�AB<ADʱ����E�����߶�AB�ϣ�
�۸������ε��ж�������֪����EF��ACʱ���ı���AECFΪ���Σ�
�ܵ�CE��AB�ҡ�BAC��45��ʱ���ı���AECFΪ�����Σ���AB��һ������һ��E
�⣺��1����ͼ1��
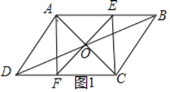
���ı���ABCDΪƽ���ı��Σ��Խ���AC��BD���ڵ�O��
��AB��DC��AB��DC��OA��OC��OB��OD��
���OAE����OCF��
�ߡ�AOE����COF��
���AOE�ա�COF��ASA����
��AE��CF��
�֡�AE��CF��
���ı���AECFΪƽ���ı��Σ�
��E��AB������λ�ã�����A��B�غϣ�ʱ���ı���AECF��Ϊƽ���ı��Σ�
��ѡ�����ȷ��
��2����ͼ2������ABC��90��,
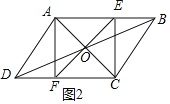
��CE��ABʱ���ı���AECFΪ���Σ�
��ͼ2�У�AB>ADʱ������һ��E, ʹ���ı���AECF�Ǿ��Σ�
��ͼ2-2�У�AB<ADʱ����E�����߶�AB�ϣ�
��ѡ��ڲ���ȷ��
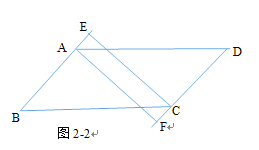
��3����ͼ3��

��EF��ACʱ���ı���AECFΪ���Σ�
��AB��AD��
����AB��һ������һ��E, ʹ���ı���AECF�Ǿ��Σ�
��ѡ�����ȷ��
��4����ͼ4��

��CE��AB�ҡ�BAC��45��ʱ���ı���AECFΪ�����Σ���ѡ�����ȷ��
�ʴ�Ϊ���٢ۢܣ�


 �����Ļ�������ҵϵ�д�
�����Ļ�������ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�˸���λͬѧ��ij������Է�����ͼΪ�˿�����IJ˵�������������IJ�ʳ�ܹ�Ϊ10�ݸǷ���x�����ϣ�y������ˣ�
��1�����ǵ����� ����A�ײͣ��� ����B�ײͣ��� ����C�ײͣ����ú�x��y�Ĵ���ʽ��ʾ����
��2����x��6����A��B��C�ײ;����ٵ���1�ݣ���������� ���ֵ�ͷ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
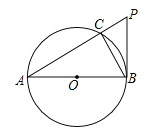
����Ŀ����ͼ��AB�ǡ�O��ֱ����PB���O�����ڵ�B������PA����O�ڵ�C������BC��
��1����֤����BAC=��CBP��
��2����֤��PB2=PCPA��
��3����AC=6��CP=3ʱ����sin��PAB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
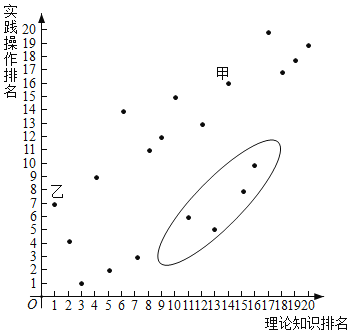
����Ŀ��ij��˾�ƻ���ļ10��������Ա�����Ƕ�20�����Ժϸ���Ա�����˲��ԣ�����������֪ʶ��ʵ�����������֣�20��ӦƸ�ߵijɼ����������ͼ��ʾ��������3���ƶϣ�
�ټײ��Գɼ��dz����㣬��ѡ�Ŀ����Ժܴ�
���ҵ�����֪ʶ������ʵ������������ǰ��
��λ����Բ�������ڵ�ӦƸ��Ӧ�ü�ǿ��רҵ����֪ʶ��ѧϰ��
���к�������_____����д��ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
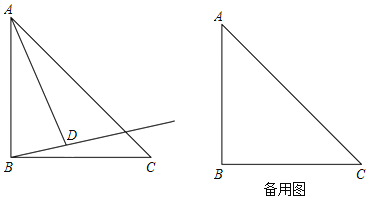
����Ŀ����ABC�У�AB��BC����ABC��90�������߶�AB�Ƶ�A��ʱ����ת����0��������90�����õ��߶�AD��������BD����C��������BD�ĶԳƵ�Ϊ��E������AE��CE��
��1�������ⲹȫͼ�Σ�
��2��������20����ֱ��д����AEC�Ķ�����
��3��д��һ������ֵ��ʹAE��![]() ʱ���߶�CE�ij�Ϊ
ʱ���߶�CE�ij�Ϊ![]() ��1����֤����
��1����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
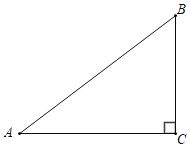
����Ŀ����ͼ����Rt��ABC�У���C��90������ACΪֱ������O��AB�ڵ�D���߶�BC����һ��P��
��1������P��ʲôλ��ʱ��ֱ��DP���O����ֻ��һ�������㣬��ȫͼ�β�˵�����ɣ�
��2���ڣ�1���������£���BP��![]() ��AD��3ʱ�����O�뾶��
��AD��3ʱ�����O�뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�һ�κ���y��x+4��ͼ����y�ύ�ڵ�A���뷴��������y��![]() ��ͼ���һ������ΪM��
��ͼ���һ������ΪM��
��1�����A�����ꣻ
��2������OM�������MOA���������2����k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���![]() �������Σ����߶�
�������Σ����߶�![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת
��ʱ����ת![]() ���õ��߶�
���õ��߶�![]() ������
������![]() ������
������![]() ��
��![]() ��
��![]() ���ӳ�����
���ӳ�����![]() ������
������![]() ��
��
��1�������ⲹȫͼ1��
��2��ֱ��д��![]() �Ķ�����
�Ķ�����
��3������![]() ���õ�ʽ��ʾ�߶�
���õ�ʽ��ʾ�߶�![]() ��
��![]() ��������ϵ����֤����
��������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
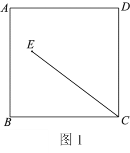
����Ŀ����ͼ��![]() �У�
��![]() ��
��
��1�����ó߹���ͼ�ķ����ڱ�![]() ��ȷ����
��ȷ����![]() ��ʹ�õ�
��ʹ�õ�![]() ����
����![]() �ľ������
�ľ������![]() �ij������������úۼ�����д������
�ij������������úۼ�����д������
��2���ڣ�1���������£���֤��![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com