
【题目】如图,以ABCD的边BC为直径的⊙O交对角线AC于点E,交CD于点F.连结BF.过点E作EG⊥CD于点G,EG是⊙O的切线.
(1)求证:ABCD是菱形;
(2)已知EG=2,DG=1.求CF的长.
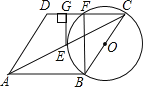
【答案】(1)见解析;(2)3
【解析】
(1)如图,连接OE,根据切线的性质得到OE⊥EG,根据平行四边形的性质得到OE∥CD∥AB,推出AB=BC,于是得到结论;
(2)如图,连接BD,由(1)得,CE:AC=1:2,得到点E是AC的中点,根据圆周角定理得到BF⊥CD,根据相似三角形的性质得到DF=2,BF=4,由勾股定理即可得到结论.
(1)证明:如图,连接OE,
∵EG是⊙O的切线,
∴OE⊥EG,
∵EG⊥CD,
∴四边形ABCD是平行四边形,
∴OE∥CD∥AB,
∴∠CEO=∠CAB,
∵OC=OE,
∴∠CEO=∠ECO,
∴∠ACB=∠CAB,
∴AB=BC,
∴ABCD是菱形;
(2)如图,连接BD,
由(1)得,OE∥CD,OC=OB,
∴AE=CE,
∴CE:AC=1:2,
∴点E是AC的中点,
∵四边形ABCD是菱形,
∴BD经过点E,
∵BC是⊙O的直径,
∴BF⊥CD,
∵EG⊥CD,
∴EG∥BF,
∴△DGE∽△DFB,
∴DG:DF=GE:BF=DE:BD=1:2,
∴DF=2,BF=4,
在Rt△BFC中,设CF=x,则BC=x+2,
由勾股定理得,x2+42=(x+2)2,
解得:x=3,
∴CF=3.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
【题目】某医药公司有A仓、B仓两个原材料仓库和甲、乙两个加工厂,其中A合、B仓共原材料22000吨,从A仓、B仓运往甲加工厂、乙加工厂的运费价如下表:

若将A仓的原材全部运往乙加T所需的费用与B仓的原材料全部运往甲加厂所需费用相同,
(1)A仓、B仓各有原材料多少吨?
(2)若甲加工厂需要从A、B两仓调运9000吨原材料,乙加工厂需要从A、B两仓调运13000原材料,且从A仓运送到甲加工厂的原材料最多9000吨,请问医药公司怎么调运可使总运费最少?求出最少运费.
查看答案和解析>>
科目:初中数学 来源: 题型:
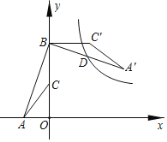
【题目】如图,点A的坐标是(﹣1,0),点B的坐标是(0,4),C为OB上任意一点,将△ABC绕点B逆时针旋转90°后得到△A′B′C′.若反比例函数y=![]() 的图象恰好经过A′B的中点D,则k=____.
的图象恰好经过A′B的中点D,则k=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
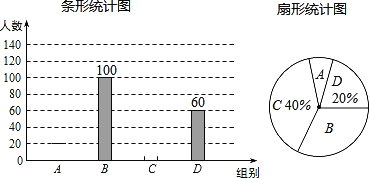
【题目】国家规定,中小学生每天在校体育活动时间不低于1小时,今年受“新冠肺炎”疫情的影响,为落实教育部“停课不停学”的要求,我市中学生进行居家线上学习,为保证广大学生的身心健康,有关部门就“你每天线上学习时在室内或室外安全区域体育锻炼时间是多少”的问题在某校开展了电话调查,随机抽查了部分学生,再根据锻炼时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如图两幅不完整统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为 人,并补全条形统计图;
(2)计算扇形统计图中A组部分所对应的扇形圆心角度数;
(3)若当天该校进行居家线上学习的学生数为1300人,请估计在当天达到国家规定体育活动时间的学生有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是Rt△ABC斜边AB的中点,点E在边AC上.△A'B′C′与△ABC关于直线BE对称,连结A′C.且∠CA′C'=90°.若AC=4,BC=3.则AE的长为_____.
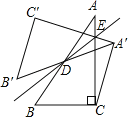
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,4),B(﹣4,0),C(﹣1,0).
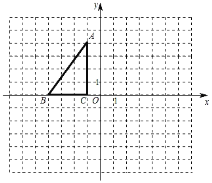
(1)△A1B1C1与△ABC关于原点O对称,画出△A1B1C1并写出点A1的坐标;
(2)△A2B2C2是△ABC绕原点O顺时针旋转90°得到的,画出△A2B2C2并写出点A2的坐标;
(3)连接OA、OA2,在△ABC绕原点O顺时针旋转90°得到的△A2B2C2的过程中,计算A变换到A2过程中的路径是多少?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长、宽均为3,高为8的长方体容器,放置在水平桌面上,里面盛有水,水面高为6,绕底面一棱长进行旋转倾斜后,水面恰好触到容器口边缘,图2是此时的示意图,则图2中水面高度为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
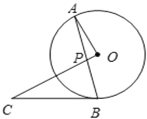
【题目】如图,AB是⊙O的弦,点C为⊙O外一点,CO⊥OA,交AB于点P,连接BC,BC=PC.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为3,OP=1,求PC的长.
(3)在(2)的条件下,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
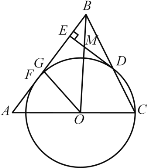
【题目】如图,在△ABC中,AB=AC=10,tan∠A=![]() ,点O是线段AC上一动点(不与点A,点C重合),以OC为半径的⊙O与线段BC的另一个交点为D,作DE⊥AB于E.
,点O是线段AC上一动点(不与点A,点C重合),以OC为半径的⊙O与线段BC的另一个交点为D,作DE⊥AB于E.
(1)求证:DE是⊙O的切线;
(2)当⊙O与AB相切于点F时,求⊙O的半径;
(3)在(2)的条件下,连接OB交DE于点M,点G在线段EF上,连接GO.若∠GOM=45°,求DM和FG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com