
分析 (1)将分母有理化即可;
(2)原式各项分母有理化,计算即可得到结果;
(3)原式各项分母有理化,计算即可得到结果.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}-\sqrt{n}$;
(2)($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2009}+\sqrt{2008}}$)•($\sqrt{2009}$+1)
=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2009}$-$\sqrt{2008}$)•($\sqrt{2009}$+1)
=($\sqrt{2009}$-1)•($\sqrt{2009}$+1)=2008;
(3)$\frac{1}{2\sqrt{1}+1\sqrt{2}}$+$\frac{1}{3\sqrt{2}+2\sqrt{3}}$+$\frac{1}{4\sqrt{3}+3\sqrt{4}}$+…+$\frac{1}{2009\sqrt{2008}+2008\sqrt{2009}}$=$\frac{1}{\sqrt{2}(\sqrt{2}+1)}$+$\frac{1}{\sqrt{6}(\sqrt{3}+\sqrt{2})}$+$\frac{1}{\sqrt{12}(\sqrt{4}+\sqrt{3})}$+…+$\frac{1}{\sqrt{2008×2009}(\sqrt{2009}+\sqrt{2008})}$
=$\frac{\sqrt{2}-1}{\sqrt{2}}$+$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{6}}$+$\frac{\sqrt{4}-\sqrt{3}}{\sqrt{12}}$+…+$\frac{\sqrt{2009}-\sqrt{2008}}{\sqrt{2009×2008}}$=$\frac{\sqrt{2}-1}{\sqrt{2}×1}$+$\frac{\sqrt{3}-\sqrt{2}}{\sqrt{3}×\sqrt{2}}$-$\frac{\sqrt{4}-\sqrt{3}}{\sqrt{4}×\sqrt{3}}$+…+$\frac{\sqrt{2009}-\sqrt{2008}}{\sqrt{2009}×\sqrt{2008}}$=1-$\frac{1}{\sqrt{2}}$+$\frac{1}{\sqrt{2}}$-$\frac{1}{\sqrt{3}}$+$\frac{1}{\sqrt{4}}$-$\frac{1}{\sqrt{3}}$+…+$\frac{1}{\sqrt{2008}}$-$\frac{1}{\sqrt{2009}}$
=1-$\frac{1}{\sqrt{2009}}$=$\frac{2009-\sqrt{2009}}{2009}$.
点评 此题考查了分母有理化,正确选择两个二次根式,使它们的积符合平方差公式是解答问题的关键.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:选择题
| A. | 6÷(-$\frac{1}{4}$)×4=6×(-4)×4 | B. | 6÷(-$\frac{1}{4}$)×4=6×(-$\frac{1}{4}$)×4 | C. | 6÷(-$\frac{1}{4}$)×4=6÷(-$\frac{1}{4}$×4) | D. | 6÷(-$\frac{1}{4}$)×4=6×(-4)÷4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 有两个内角是60°的三角形 | |
| B. | 有两边相等且是轴对称图形的三角形 | |
| C. | 三边都相等的三角形 | |
| D. | 有一个角是60°且是轴对称图形的三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,AC=BC,点D为AB中点,点E在BA的延长线上,过B作BF⊥EC交EC延长线于F,交DC延长线于G.
如图,在△ABC中,∠ACB=90°,AC=BC,点D为AB中点,点E在BA的延长线上,过B作BF⊥EC交EC延长线于F,交DC延长线于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
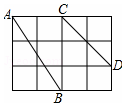 如图,在4×3正方形网格中,每个小正方形的边长都是1
如图,在4×3正方形网格中,每个小正方形的边长都是1查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+1)(a-1)=a2-1 | B. | x2-4=(x+2)(x-2) | ||
| C. | x2-4+3x=(x+2)(x-2)+3x | D. | x2-1=x(x-$\frac{1}{x}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点E,F为正方形ABCD边BC,CD上的点,且△CEF的周长等于正方形ABCD周长的一半.
如图,点E,F为正方形ABCD边BC,CD上的点,且△CEF的周长等于正方形ABCD周长的一半.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com