
【题目】如图,已知∠B=∠C.
(1)若AD∥BC,则AD平分∠EAC吗?请说明理由.
(2)若∠B+∠C+∠BAC=180°,AD平分∠EAC,则AD∥BC吗?请说明理由.

科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点C,与y轴交于点B,点A(1,3),点B(0,2).连接AO
(1)求直线AB的解析式;
(2)求三角形AOC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米):请根据上表的内容解答下列问题:
表示立方米):请根据上表的内容解答下列问题:
(1)填空:若该户居民![]() 月份用水
月份用水![]() ,则应收水费___________元;
,则应收水费___________元;
(2)若该户居民![]() 月份用水
月份用水![]() (其中
(其中![]() ),则应收水费多少元?
),则应收水费多少元?
价目表
每月用水量 | 单价 |
不超过6 | 2元/ |
超出6 | 4元/ |
超出10 | 8元/ |
(3)若该户居民![]() 、
、![]() 两个月共用水
两个月共用水![]() (
(![]() 月份用水量超过了
月份用水量超过了![]() 月份),设
月份),设![]() 月份用水
月份用水![]() ,求该户居民
,求该户居民![]() 、
、![]() 两个月共交水费多少元?(答案可含有
两个月共交水费多少元?(答案可含有![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m,另一边减少了2m,剩余空地的面积为18m2 , 求原正方形空地的边长.设原正方形的空地的边长为xm,则可列方程为( ) 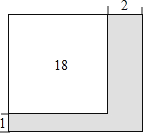
A.(x+1)(x+2)=18
B.x2﹣3x+16=0
C.(x﹣1)(x﹣2)=18
D.x2+3x+16=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=10,AC=2![]() ,BC边上的高AD=6,则另一边BC等于_______.
,BC边上的高AD=6,则另一边BC等于_______.
【答案】10或6
【解析】试题解析:根据题意画出图形,如图所示,

如图1所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD+CD=8+2=10;
如图2所示,AB=10,AC=2![]() ,AD=6,
,AD=6,
在Rt△ABD和Rt△ACD中,
根据勾股定理得:BD=![]() =8,CD=
=8,CD=![]() =2,
=2,
此时BC=BD-CD=8-2=6,
则BC的长为6或10.
【题型】填空题
【结束】
12
【题目】在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)指出数轴上 A、B、C、D、E 各点分别表示什么数;
(2)按从小到大顺序排列,将它们用“<”号连接起来;
(3)写出离 C 点 3 个单位的点表示的数;
(4)写出离 C 点 m 个单位的点表示的数(m>0).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择.
方案一:每千克种子价格为4元,均不打折;
方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次购买超过3千克,则超出部分的种子打七折.
(1)请分别求出方案一、方案二中购买的种子数量x(千克)与付款金额y(元)之间的函数关系式;
(2)若你去购买一定量的种子,你会怎样选择方案?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为
的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为![]() 其中
其中![]() .
.
![]() 四边形ABCD的是______
四边形ABCD的是______![]() 填写四边形ABCD的形状
填写四边形ABCD的形状![]()
![]() 当点A的坐标为
当点A的坐标为![]() 时,四边形ABCD是矩形,求m,n的值.
时,四边形ABCD是矩形,求m,n的值.
![]() 试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com