
【题目】如图,四边形ABCD内接于⊙O,点E在CB的延长线上,连接AC,AE,∠ACB=∠BAE=45°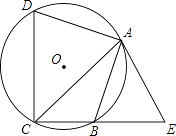
(1)求证:AE是⊙O的切线;
(2)若 AB=AD,AC=2 ![]() ,tan∠ADC=3,求CD的长.
,tan∠ADC=3,求CD的长.
【答案】
(1)
证明:
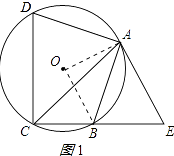
连接OA、OB,如图1所示:
∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BAE=45°,
∴∠OAE=∠OAB+∠BAE=90°,
∴AE⊥OA,
∴AE是⊙O的切线
(2)
解:
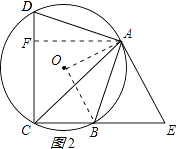
作AF⊥CD于F,如图2所示:
∵AB=AD,
∴ ![]() ,
,
∴∠ACB=∠ACD=45°,
∵AF⊥CD,
∴∠AFC=∠AFD=90°,
∵AC=2 ![]() ,
,
∴在Rt△AFC中,AF=CF=ACsin∠ACF=2 ![]() ×
× ![]() =2,
=2,
∵在Rt△AFD中,tan∠ADC= ![]() =3,
=3,
∴DF= ![]() ,
,
∴CD=CF+DF=2+ ![]() =
= ![]() .
.
【解析】(1)连接OA、OB,由圆周角定理得出∠AOB=2∠ACB=90°,由等腰直角三角形的性质得出∠OAB=∠OBA=45°,求出∠OAE=∠OAB+∠BAE=90°,即可得出结论;(2)作AF⊥CD于F,证出 ![]() ,由圆周角定理得出∠ACB=∠ACD=45°,由三角函数求出AF=CF=ACsin∠ACF=2,DF=
,由圆周角定理得出∠ACB=∠ACD=45°,由三角函数求出AF=CF=ACsin∠ACF=2,DF= ![]() ,即可得出CD的长.
,即可得出CD的长.
【考点精析】认真审题,首先需要了解切线的判定定理(切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】王大爷家有一块梯形形状土地,如图,AD∥BC , 对角线AD , BC相交于点O , 王大爷量得AD长3米,BC长9米,王大爷准备在△AOD处种大白菜,那么王大爷种大白菜的面积与整个土地的面积比为( ).
A.1:14
B.3:14
C.1:16
D.3:16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.若设小道的宽为x米,则可列方程为 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组管道如图1所示,其中四边形ABCD是矩形,O是AC的中点,管道由AB,BC,CD,DA,OA,OB,OC,OD组成,在BC的中点M 处放置了一台定位仪器.一个机器人在管道内匀速行进,对管道进行检测.设机器人行进的时间为x,机器人与定位仪器之间的距离为y,表示y与x的函数关系的图象大致如图2所示,则机器人的行进路线可能为( )
A.A→O→D
B.B→O→D
C.A→B→O
D.A→D→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A的坐标为(1,0),P是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).
(1)点( ![]() ,
, ![]() )的“双角坐标”为;
)的“双角坐标”为;
(2)若点P到x轴的距离为 ![]() ,则m+n的最小值为 .
,则m+n的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A的坐标为(1,0),P是第一象限内任意一点,连接PO,PA,若∠POA=m°,∠PAO=n°,则我们把(m°,n°)叫做点P 的“双角坐标”.例如,点(1,1)的“双角坐标”为(45°,90°).
(1)点( ![]() ,
, ![]() )的“双角坐标”为;
)的“双角坐标”为;
(2)若点P到x轴的距离为 ![]() ,则m+n的最小值为 .
,则m+n的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究函数y=x+ ![]() 的图象与性质
的图象与性质
(1)函数y=x+ ![]() 的自变量x的取值范围是;
的自变量x的取值范围是;
(2)下列四个函数图象中,函数y=x+ ![]() 的图象大致是
的图象大致是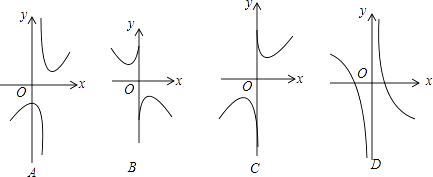
(3)对于函数y=x+ ![]() ,求当x>0时,y的取值范围.
,求当x>0时,y的取值范围.
请将下面求解此问题的过程补充完整:
解:∵x>0
∴y=x+ ![]()
=( ![]() )2+(
)2+( ![]() )2
)2
=( ![]() ﹣
﹣ ![]() )2+
)2+
∵( ![]() ﹣
﹣ ![]() )2≥0,
)2≥0,
∴y .
(4)若函数y= ![]() ,则y的取值范围是
,则y的取值范围是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y1=mx2+(m﹣3)x﹣3(m>0)与x轴交于A、B两点,且点A在点B的左侧,与y轴交于点C,OB=OC. 
(1)求这条抛物线的表达式;
(2)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,若点C在直线y2=﹣3x+t上,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为菱形ABCD对角线的交点,DE∥AC,CE∥BD. 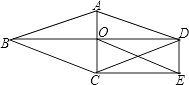
(1)试判断四边形OCED的形状,并说明理由;
(2)若AC=6,BD=8,求线段OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com