
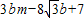 的值达到最小时,求BC的长.
的值达到最小时,求BC的长.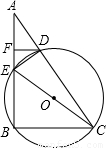
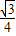 m代入代数式
m代入代数式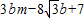 可得:
可得: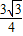 m2-12m+7,当它有最小值时,m=-
m2-12m+7,当它有最小值时,m=-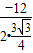 =
=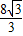 .因为△CEB与△CBD全等,可推出EC=2EB,利用勾股定理可得CB的式子,再分别将m的值代入即可求得CB的值.
.因为△CEB与△CBD全等,可推出EC=2EB,利用勾股定理可得CB的式子,再分别将m的值代入即可求得CB的值.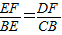 ;
;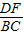 =
= ,BE=BF-EF,
,BE=BF-EF,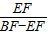 =
= ,
, ,BF=
,BF=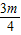 ;
;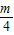 •
•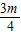 =b2;
=b2;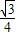 m(b>0).
m(b>0).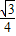 m代入代数式
m代入代数式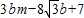 得:
得: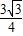 m2-6m+7,
m2-6m+7,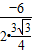 =
=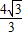 ;
; AC,
AC, AC,
AC,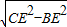 ;
;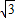 BE=
BE=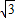
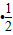 m;
m;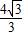 ,
,

科目:初中数学 来源:2000年浙江省宁波市中考数学试卷(解析版) 题型:解答题
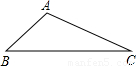
查看答案和解析>>
科目:初中数学 来源:2000年浙江省宁波市中考数学试卷(解析版) 题型:选择题
 ,若AC=
,若AC=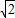 ,则菱形移动的距离AA′是( )
,则菱形移动的距离AA′是( )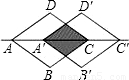
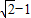
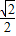

查看答案和解析>>
科目:初中数学 来源:2000年浙江省宁波市中考数学试卷(解析版) 题型:选择题
查看答案和解析>>
科目:初中数学 来源:2000年浙江省宁波市中考数学试卷(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com