
【题目】2019年沈阳国际马拉松赛事设有“马拉松”(A),“半程马拉松”(B),“10公里跑”(C),“迷你马拉松”(D)四个项目,小明和小亮参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到四个项目组,被分配到每个项目组的机会是相同的.
(1)小明被分配到“马拉松”(A)项目组的概率为 ;
(2)利用画树状图或列表法求小明和小亮被分配到同一个项目组进行志愿服务的概率.(项目名称可用字母表示)
 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
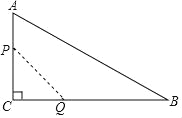
【题目】如图,在Rt△ABC中,∠C=90°,AC=12cm,BC=24cm.动点P从点A开始沿边AC向点C以2cm/s的速度移动;动点Q从点C开始沿边CB向点B以4cm/s的速度移动.如果P,Q两点同时出发.
(1)经过几秒,△PCQ的面积为32cm2?
(2)若设△PCQ的面积为S,运动时间为t,请写出当t为何值时,S最大,并求出最大值;
(3)当t为何值时,以P,C,Q为顶点的三角形与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】活动1:
在一只不透明的口袋中装有标号为1,2,3的3个小球,这些球除标号外都相同,充分搅匀,甲、乙、丙三位同学按丙→甲→乙的顺序依次从袋中各摸出一个球(不放回),摸到1号球胜出,请你通过画树状图或列表计算甲胜出的概率.(注:丙→甲→乙表示丙第一个摸球,甲第二个摸球,乙最后一个摸球)
活动2:
在一只不透明的口袋中装有标号为1,2,3,4的4个小球,这些球除标号外都相同,充分搅匀,请你对甲、乙、丙三名同学规定一个摸球顺序: → → ,他们按这个顺序从袋中各摸出一个球(不放回),摸到1号球胜出,通过画树状图或列表求每位同学胜出的概率分别是多少.
猜想:
在一只不透明的口袋中装有标号为1,2,3,…,![]() (
(![]() 为正整数)的
为正整数)的![]() 个小球,这些球除标号外都相同,充分搅匀,甲、乙、丙三名同学按任意顺序从袋中各摸出一个球(不放回),摸到1号球胜出,猜想:直接写出这三名同学每人胜出的概率之间的大小关系.
个小球,这些球除标号外都相同,充分搅匀,甲、乙、丙三名同学按任意顺序从袋中各摸出一个球(不放回),摸到1号球胜出,猜想:直接写出这三名同学每人胜出的概率之间的大小关系.
由此你能得到什么活动经验?(写出一个即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数![]() (a,b为常数,且
(a,b为常数,且![]() )与反比例函数
)与反比例函数![]() (m为常数,且
(m为常数,且![]() )的图象交于点A(﹣2,1)、B(1,n).
)的图象交于点A(﹣2,1)、B(1,n).
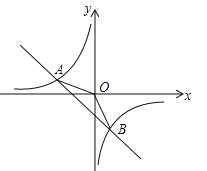
(1)求反比例函数和一次函数的解析式;
(2)连结OA、OB,求△AOB的面积;
(3)直接写出当![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣(x﹣m)2+4(m>0)的顶点为A,与直线x=![]() 相交于点B,点A关于直线x=
相交于点B,点A关于直线x=![]() 的对称点为C.
的对称点为C.
(1)若抛物线y=﹣(x﹣m)2+4(m>0)经过原点,求m的值.
(2)点C的坐标为 .用含m的代数式表示点B到直线AC的距离为 .
(3)将y=﹣(x﹣m)2+4(m>0,且x≥![]() )的函数图象记为图象G,图象G关于直线x=
)的函数图象记为图象G,图象G关于直线x=![]() 的对称图象记为图象H.图象G与图象H组合成的图象记为图象M.
的对称图象记为图象H.图象G与图象H组合成的图象记为图象M.
①当图象M与x轴恰好有三个交点时,求m的值.
②当△ABC为等腰直角三角形时,直接写出图象M所对应的函数值小于0时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A(0,4),B(1,m)都在直线y=﹣2x+b上,反比例函数y=![]() (x>0)的图象经过点B.
(x>0)的图象经过点B.
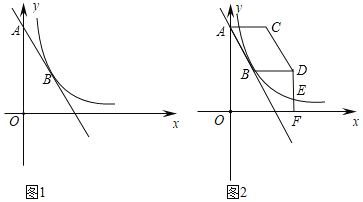
(1)直接写出m和k的值;
(2)如图2,将线段AB向右平移n个单位长度(n≥0),得到对应线段CD,连接AC,BD.
①在平移过程中,若反比例函数图象与线段AB有交点,求n的取值范围;
②在平移过程中,连接BC,若△BCD是直角三角形,请直接写出所有满足条件n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角![]() 中,
中,![]() ,
,![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.
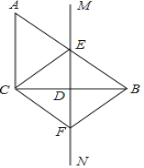
(1)求证:![]() ;
;
(2)求证:四边形![]() 是菱形.
是菱形.
(3)当![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形,请说明理由.
是正方形,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面内容,并解答问题:
杨辉和他的一个数学问题

我国古代对代数的研究,特别是对方程的解法研究有着优良的传统并取得了重要成果.
杨辉,字谦光,钱塘(今浙江杭州)人,南宋杰出的数学家和数学教育家,杨辉一生留下了大量的著述,他著名的数学书共五种二十一卷,它们是:《详解九章算法》12卷(1261年),《日用算法》2卷(1262年),《乘除通变本末》3卷(1274年,第3卷与他人合编),《田(杨辉,南宋数学家)亩比类乘除捷法》2卷(1275年),《续古摘奇算法》2卷(1275年,与他人合编),其中后三种为杨辉后期所著,一般称之为《杨辉算法》.下面是杨辉在1275年提出的一个问题(选自杨辉所著《田亩比类乘除捷法》):
直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),问阔及长各几步.
请你用学过的知识解决这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.

(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com