
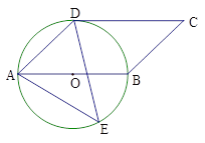
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上任意一点,且CD切⊙O于点D.
(1)试求∠AED的度数.
(2)若⊙O的半径为![]() cm,试求△ADE面积的最大值.
cm,试求△ADE面积的最大值.
【答案】
【1】 45° 或135
【2】 ![]()
【解析】
(1)利用平行四边形的性质以及切线的性质和圆周角定理求出即可;
(2)利用当三角形高度最大时面积最大,求出EF的长即可得出答案.
解答:
(1)连接DO,DB,
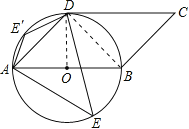
∵四边形ABCD是平行四边形,CD切⊙O于点D。
∴DO⊥DC,
∴∠DBA=45°,
∵∠DBA=∠E,
∴∠E=45°,
当E′点在如图所示位置,即可得出∠AE′D=180°-45°=135°,
∴∠AED的度数为45 °或135°。
(2)当∠AED=45°,且E在AD垂直平分线上时,△ADE的面积最大。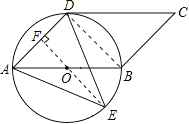
∵∠AED=45°,
∴∠DAB=∠DBA=45°,∠ADB=90°,
∵⊙O的半径为3![]() cm,
cm,
∴AB=6![]() cm,
cm,
∴AD=DB=6,
AF=FO=3,
∴S△ADE=1/2×AD×(FO+EO)=1/2×6×(3+3![]() )=(9+9
)=(9+9![]() )cm 2。
)cm 2。


科目:初中数学 来源: 题型:
【题目】已知y1=a1x2+b1x+c1,y2=a2x2+b2x+c2且满足![]() (k≠0,1).则称抛物线y1,y2互为“友好抛物线”,则下列关于 “友好抛物线”的说法不正确的是( )
(k≠0,1).则称抛物线y1,y2互为“友好抛物线”,则下列关于 “友好抛物线”的说法不正确的是( )
A. y1,y2开口方向、开口大小不一定相同
B. 因为y1,y2的对称轴相同
C. 如果y2的最值为m,则y1的最值为km
D. 如果y2与x轴的两交点间距离为d,则y1与x轴的两交点间距离为|k|d
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点C是⊙O中直径AB上的一个动点,过点C作CD⊥AB交⊙O于点D,点M是直径AB上一固定点,作射线DM交⊙O于点N.已知AB=6cm,AM=2cm,设线段AC的长度为xcm,线段MN的长度为ycm.
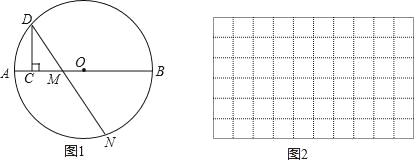
小东根据学习函数的经验,对函数y随自变量的变化而变化的规律进行了探索.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 4 | 3.3 | 2.8 | 2.5 |
| 2.1 | 2 |
(说明:补全表格时相关数值保留一位小数)
(2)在图2中建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当AC=MN时,x的取值约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,老师要求学生在5×5的正方形ABCD网格中(小正方形的边长为1)画等腰三角形,要求三个顶点都在格点上(小正方形的顶点称为格点),用实线画四种图形,且分别符合下列各条件:
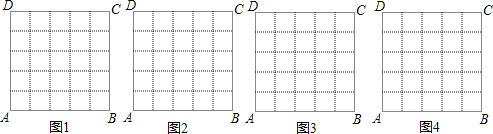
(1)面积为2(画在图1中);
(2)面积为4,且三边与AB或AD都不平行(画在图2中);
(3)面积为5,且三边与AB或AD都不平行(画在图3中);
(4)面积为![]() ,且三边与AB或AD都不平行(画在图4中).
,且三边与AB或AD都不平行(画在图4中).
查看答案和解析>>
科目:初中数学 来源: 题型:
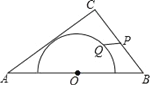
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
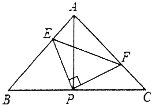
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出下列四个结论:
①AE=CF;
②△EPF是等腰直角三角形;
③EF=AB;
④![]() ,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有________(把你认为正确的结论的序号都填上).
,当∠EPF在△ABC内绕顶点P旋转时(点E不与A、B重合),上述结论中始终正确的有________(把你认为正确的结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,不能判定四边形ABCD为矩形的是( )
A.AB∥CD,AB=CD,AC=BDB.∠A=∠B=∠D=90°
C.AB=BC,AD=CD,且∠C=90°D.AB=CD,AD=BC,∠A=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )

A. 40° B. 45° C. 60° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
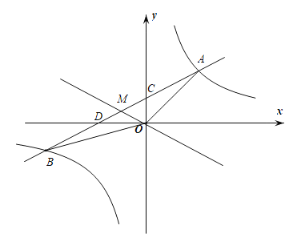
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 相交于
相交于![]() 、
、![]() 两点,与
两点,与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,已知
两点,已知![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求一次函数和反比例函数的解析式;
(2)连接![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 的中点,直线
的中点,直线![]() 向上平移
向上平移![]() 个单位将
个单位将![]() 的面积分成
的面积分成![]() 两部分,求
两部分,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com