
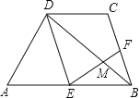
【题目】 如图,梯形ABCD中,AB//CD,且AB=2CD,E,F分别是AB,BC的中点.
EF与BD相交于点M.
(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,△ABC的顶点A(-3,0)、B(0,3),AD⊥BC交BC于D点,交y轴正半轴于点E(0,t)
(1)当t=1时,求C点的坐标;
(2)如图2,求∠ADO的度数;
(3)如图3,已知点P(0,2),若PQ⊥PC,PQ=PC,求Q的坐标(用含t的式子表示).
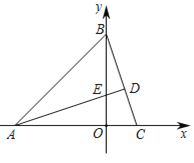
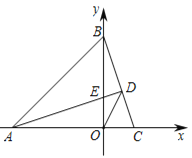
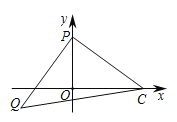
图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A. 同号数相乘,符号不变
B. 两数相乘,若积为负数,则这两个数都为负
C. 两数相乘,若积为0,则两个因数中至少有一个为0
D. 两数相乘,积一定大于每一个因数
查看答案和解析>>
科目:初中数学 来源: 题型:
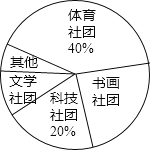
【题目】某校计划成立学生社团,要求每一位学生都选择一个社团,为了了解学生对不同社团的喜爱情况,学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查,规定每人必须并且只能在“文学社团”、“科学社团”、“书画社团”、“体育社团”和“其他”五项中选择一项,并将统计结果绘制了如下两个不完整的统计图表.
社团名称 | 人数 |
文学社团 | 18 |
科技社团 | a |
书画社团 | 45 |
体育社团 | 72 |
其他 | b |
请解答下列问题:
(1)a= ,b= ;
(2)在扇形统计图中,“书画社团”所对应的扇形圆心角度数为 ;
(3)若该校共有3000名学生,试估计该校学生中选择“文学社团”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若正比例函数的图象经过点(﹣1,2),则这个图象必经过点( )
A. (1,2) B. (﹣1,﹣2) C. (2,﹣1) D. (1,﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com