
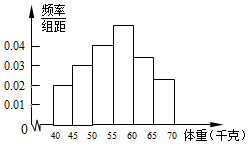
 为了解全区5000名初中毕业生的体重情况,随机抽测了400名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为1500人.
为了解全区5000名初中毕业生的体重情况,随机抽测了400名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为1500人. 分析 先根据频率分布直方图,得到从左至右前四组的频率,进而得出后两组的频率之和,最后根据总数×频率,即可得到体重不小于60千克的学生人数.
解答 解:∵从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,
∴从左至右前四组的频率依次为0.02×5=0.1、0.03×5=0.15、0.04×5=0.2、0.05×5=0.25,
∴后两组的频率之和为:1-0.1-0.15-0.2-0.25=0.3,
∴体重不小于60千克的学生人数约为:5000×0.3=1500人,
故答案为:1500.
点评 本题考查了频数分布图和频率分布直方图的知识,根据频率、频数及样本容量之间的关系进行正确的运算是解题的关键.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:解答题
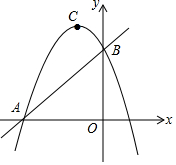 如图,直线y=x+n与x轴交于点A,与y轴交于点B(点A与点B不重合),抛物线y=-$\frac{1}{2}$x2-2x+c经过点A、B,抛物线的顶点为C.
如图,直线y=x+n与x轴交于点A,与y轴交于点B(点A与点B不重合),抛物线y=-$\frac{1}{2}$x2-2x+c经过点A、B,抛物线的顶点为C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com