
【题目】某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分),A组:75≤x<80;B组:80≤x<85;C组:85≤x<90;D组:90≤x<95;E组:95≤x<100.并绘制出如图两幅不完整的统计图.

请根据图中信息,解答下列问题:
(1)参加初赛的选手共有 名,请补全频数分布直方图;
(2)扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?
(3)学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中一名男生和一名女生的概率.
【答案】(1)40;(2)108°,15%;(3)![]() .
.
【解析】试题分析:(1)用A组人数除以A组所占百分比得到参加初赛的选手总人数,用总人数乘以B组所占百分比得到B组人数,从而补全频数分布直方图;
(2)用360度乘以C组所占百分比得到C组对应的圆心角度数,用E组人数除以总人数得到E组人数占参赛选手的百分比;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好抽到一男生和一女生的情况,再利用概率公式即可求得答案.
试题解析:解:(1)参加初赛的选手共有:8÷20%=40(人),B组有:40×25%=10(人).
频数分布直方图补充如下:
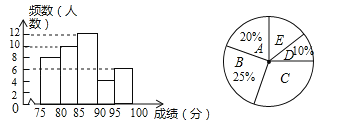
故答案为:40;
(2)C组对应的圆心角度数是:360°×![]() =108°,E组人数占参赛选手的百分比是:
=108°,E组人数占参赛选手的百分比是: ![]() ×100%=15%;
×100%=15%;
(3)画树状图得:
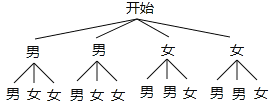
∵共有12种等可能的结果,抽取的两人恰好是一男生和一女生的有8种结果,∴抽取的两人恰好是一男生和一女生的概率为![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】用配方法解下列方程:
(1)4x2 -4x -1 = 0; (2)7x2 -28x +7= 0.
(3) ![]() x2-x-4=0 (4) 3x2-45=30x
x2-x-4=0 (4) 3x2-45=30x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,一次函数y=(1-3k)x+2k-1,试回答:
(1)k为何值时,y随x的增大而减小?
(2)k为何值时,图像与y轴交点在x轴上方?
(3) 若一次函数y=(1-3k)x+2k-1经过点(3,4).请求出一次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了乘法公式![]() 后,老师向同学们提出了如下问题:
后,老师向同学们提出了如下问题:
①将多项式x2+4x+3因式分解;
②求多项式x2+4x+3的最小值.

请你运用上述的方法解决下列问题:
(1)将多项式x2+8x-20因式分解;
(2)求多项式x2+8x-20的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?

(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强建设“经济强、环境美、后劲足、群众富”的实力城镇,聚力脱贫攻坚,全面完成脱贫任务,某乡镇特制定一系列帮扶计划。现决定将A、B两种类型鱼苗共320箱运到某村养殖,其中A种鱼苗比B种鱼苗多80箱。
(1)求A种鱼苗和B种鱼苗各多少箱?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批鱼苗全部运往同一目的地。已知甲种货车最多可装A种鱼苗40箱和B种鱼苗10箱,乙种货车最多可装A种鱼苗和B种鱼苗各20箱。如果甲种货车每辆需付运输费4000元,乙种货车每辆需付运输费3600元,则安排甲、乙两种货车有哪几种不同的方案?并说明选择哪种方案可使运输费最少?最少运输费是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
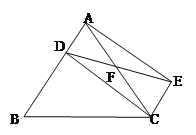
【题目】如图,D是△ABC的边AB上一点,CE∥AB,DE交AC于点F,若FA=FC.
(1)求证:四边形ADCE是平行四边形;
(2)若AE⊥EC,EF=EC=1,求四边形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长为20cm,宽为8cm的长方形白纸,按如图所示的方式粘合起来,粘合部分的宽为3cm.

(1)根据题意,将下面的表格补充完整.

(2)直接写出y与x的关系式.
(3)要使粘合后的长方形总面积为1656cm2,则需用多少张这样的白纸?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣6x+m+4=0有两个实数根x1,x2.
(1)求m的取值范围;
(2)若x1,x2满足2x1=|x2|+3,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com