
【题目】阅读材料,并回答下列问题
如图1,以AB为轴,把△ABC翻折180°,可以变换到△ABD的位置;
如图2,把△ABC沿射线AC平移,可以变换到△DEF的位置.像这样,其中的一个三角形是另一个三角形经翻折、平移等方法变换成的,这种只改变位置,不改变形状大小的图形变换,叫三角形的全等变换.班里学习小组针对三角形的全等变换进行了探究和讨论
(1)请你写出一种全等变换的方法(除翻折、平移外), .
(2)如图2,前进小组把△ABC沿射线AC平移到△DEF,若平移的距离为2,且AC=5,则DC= .
(3)如图3,圆梦小组展开了探索活动,把△ABC纸片沿DE折叠,使点A落在四边形BCDE内部点A′的位置,且得出一个结论:2∠A′=∠1+∠2.请你对这个结论给出证明.
(4)如图4,奋进小组则提出,如果把△ABC纸片沿DE折叠,使点A落在四边形BCDE外部点A′的位置,此时∠A′与∠1、∠2之间结论还成立吗?若成立,请给出证明,若不成立,写出正确结论并证明.

【答案】(1)旋转;(2)3;(3)见解析;(4)不成立,正确结论:∠2﹣∠1=2∠A',见解析
【解析】
(1)由题意根据三种全等变换翻折、平移、旋转的定义进行判断即可;
(2)根据平移的距离的定义可知AD=2,则DC=AC﹣AD进行求解即可;
(3)根据轴对称及三角形内角和定理进行分析即可得出结论;
(4)由题意根据轴对称及三角形内角和定理,进行分析即可得出结论.
解:(1)除翻折、平移外全等变换的方法还有旋转;
故答案为:旋转.
(2)∵AD=2,AC=5,
∴DC=AC﹣AD=5﹣2=3;
故答案为:3.
(3)∵把△ADE沿DE翻折,得到△A'DE,
∴△ADE≌△A'DE,
∴∠ADE=∠A'DE,∠AED=∠A'ED,
在△DEA'中,∠A'=180°﹣(∠A'DE+∠A'ED);
由平角定义知,∠2=180°﹣∠A'DA=180°﹣2∠A'DE,
∠1=180°﹣∠A'EA=180°﹣2∠A'ED,
∴∠1+∠2=180°﹣2∠A'DE+180°﹣2∠A'ED=2(180°﹣∠A'ED﹣∠A'DE),
∴2∠A′=∠1+∠2.
(4)∠2﹣∠1=2∠A',
理由如下:
∵把△ADE沿DE翻折,得到△A'DE,
∴△ADE≌△A'DE,
∴∠ADE=∠A'DE,∠AED=∠A'ED,
在△DEA'中,∠A'=180°﹣(∠A'DE+∠A'ED),
由平角定义知,∠2=180°﹣∠A'DA=180°﹣2∠A'DE,∠1=2∠A'ED﹣180°,
∴∠2﹣∠1=(180°﹣2∠A'DE)﹣(2∠A'ED﹣180°)=180°-(∠A'DE+∠A'ED),
∴∠2﹣∠1=2∠A'.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
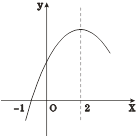
【题目】二次函数![]() 的部分图象如图③所示,图象过点(-1,0),对称轴为直线
的部分图象如图③所示,图象过点(-1,0),对称轴为直线![]() =2,则下列结论中正确的个数有( )
=2,则下列结论中正确的个数有( )
①4![]() +b=0;②
+b=0;②![]() ;③若点A(-3,
;③若点A(-3, ![]() ),点B(-
),点B(-![]() ,
, ![]() ),点C(5,
),点C(5, ![]() )在该函数图象上,则
)在该函数图象上,则![]() <
<![]() <
<![]() ;④若方程
;④若方程![]() 的两根为
的两根为![]() 和
和![]() ,且
,且![]() <
<![]() ,则
,则![]() <-1<5<
<-1<5<![]() .
.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家旅行社为了吸引更多的顾客,分别推出赴某地旅游的团体(多于4人)优惠办法.甲旅行社的优惠办法是:买4张全票,其余人按半价优惠;乙旅行社的优惠办法是:所有人都打七五折优惠.已知这两家旅行社的原价均为每人1000元,那么随着团体人数的变化,哪家旅行社的收费更优惠.
查看答案和解析>>
科目:初中数学 来源: 题型:
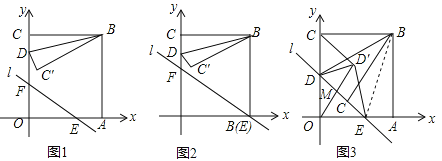
【题目】(2016浙江省衢州市)如图1,在直角坐标系xoy中,直线l:y=kx+b交x轴,y轴于点E,F,点B的坐标是(2,2),过点B分别作x轴、y轴的垂线,垂足为A、C,点D是线段CO上的动点,以BD为对称轴,作与△BCD或轴对称的△BC′D.
(1)当∠CBD=15°时,求点C′的坐标.
(2)当图1中的直线l经过点A,且![]() 时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
时(如图2),求点D由C到O的运动过程中,线段BC′扫过的图形与△OAF重叠部分的面积.
(3)当图1中的直线l经过点D,C′时(如图3),以DE为对称轴,作于△DOE或轴对称的△DO′E,连结O′C,O′O,问是否存在点D,使得△DO′E与△CO′O相似?若存在,求出k、b的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花卉种植基地欲购进甲、乙两种君子兰进行培育。若购进甲种2株,乙种3株,则共需成本l700元;若购进甲种3株,乙种l株.则共需成本l500元。
(1)求甲、乙两种君子兰每株成本分别为多少元?
(2)该种植基地决定在成本不超过30000元的前提下购入甲、乙两种君子兰,若购入乙种君子兰的株数比甲种君子兰的3倍还多10株,求最多购进甲种君子兰多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图①在等边△ABC和等边△ADE中,连接BD,CE,易证:△ABD≌△ACE;
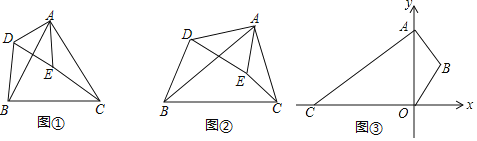
(探究)如图②△ABC与△ADE中,∠BAC=∠DAE,∠ABC=∠ADE,求证:△ABD∽△ACE;
(应用)如图③,点A的坐标为(0,6),AB=BO,∠ABO=120°,点C在x轴上运动,在坐标平面内作点D,使AD=CD,∠ADC=120°,连结OD,则OD的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,把表示数![]() 的点称为基准点,记作点
的点称为基准点,记作点![]() .对于两个不同的点
.对于两个不同的点![]() 和
和![]() ,若点
,若点![]() 、点
、点![]() 到点
到点![]() 的距离相等,则称点
的距离相等,则称点![]() 和点
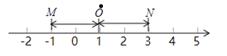
和点![]() 互为基准变换点.例如:下图中,点
互为基准变换点.例如:下图中,点![]() 表示数
表示数![]() ,点N表示数
,点N表示数![]() ,它们与基准点
,它们与基准点![]() 的距离都是
的距离都是![]() 个单位长度,点
个单位长度,点![]() 与点
与点![]() 互为基准变换点.
互为基准变换点.
(1)已知点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 与点
与点![]() 互为基准变换点.
互为基准变换点.
①若![]() ,则
,则![]() _______ ;
_______ ;
②用含![]() 的式子表示
的式子表示![]() ,则
,则![]() _____;
_____;
(2)对点![]() 进行如下操作:先把点
进行如下操作:先把点![]() 表示的数乘以
表示的数乘以![]() ,再把所得数表示的点沿着数轴向左移动
,再把所得数表示的点沿着数轴向左移动![]() 个单位长度得到点
个单位长度得到点![]() .若点
.若点![]() 与点
与点![]() 互为基准变换点,则点
互为基准变换点,则点![]() 表示的数是_____________;
表示的数是_____________;
(3)点![]() 在点
在点![]() 的左边,点
的左边,点![]() 与点
与点![]() 之间的距离为
之间的距离为![]() 个单位长度.对
个单位长度.对![]() 、
、![]() 两点做如下操作:点
两点做如下操作:点![]() 沿数轴向右移动
沿数轴向右移动![]() 个单位长度得到
个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,点
的基准变换点,点![]() 沿数轴向右移动
沿数轴向右移动![]() 个单位长度得到
个单位长度得到![]() ,
,![]() 为
为![]() 的基准变换点,……,依此顺序不断地重复,得到
的基准变换点,……,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .
.![]() 为
为![]() 的基准变换点,将数轴沿原点对折后
的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,
,![]() 为
为![]() 的基准变换点,将数轴沿原点对折后
的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,……,依此顺序不断地重复,得到
,……,依此顺序不断地重复,得到![]() ,
,![]() ,…,
,…,![]() .若无论
.若无论![]() 为何值,
为何值,![]() 与
与![]() 两点间的距离都是
两点间的距离都是![]() ,则
,则![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
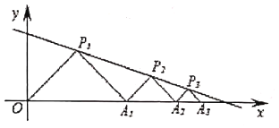
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() ,…都是等腰直角三角形,其直角顶点
,…都是等腰直角三角形,其直角顶点![]() ,
,![]() ,
,![]() ,…均在直线
,…均在直线![]() 上.设
上.设![]() ,
,![]() ,
,![]() ,…的面积分别为
,…的面积分别为![]() ,
,![]() ,
,![]() ,…,根据图形所反映的规律,
,…,根据图形所反映的规律,![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
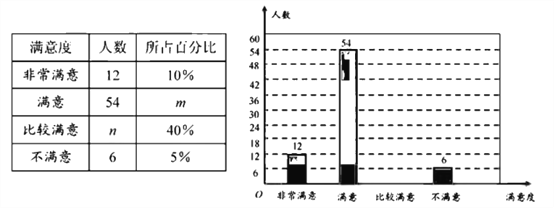
根据图表信息,解答下列问题:
(1)本次调查的总人数为 ,表中![]() 的值为 ;
的值为 ;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com