
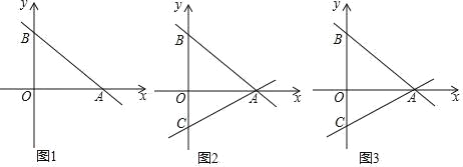
【题目】如图1,平面直角坐标系中,直线AB:y=﹣![]() x+b交x轴于点A(8,0),交y轴正半轴于点B.
x+b交x轴于点A(8,0),交y轴正半轴于点B.
(1)求点B的坐标;
(2)如图2,直线AC交y轴负半轴于点C,AB=BC,P为线段AB上一点,过点P作y轴的平行线交直线AC于点Q,设点P的横坐标为t,线段PQ的长为d,求d与t之间的函数关系式;
(3)在(2)的条件下,M为CA延长线上一点,且AM=CQ,在直线AC上方的直线AB上是否存在点N,使△QMN是以QM为斜边的等腰直角三角形?若存在,请求出点N的坐标及PN的长度;若不存在,请说明理由.
【答案】(1) B(0,6);(2) d=﹣![]() t+10;(3)见解析.
t+10;(3)见解析.
【解析】(1)把A(8,0)代入y=﹣![]() x+b,可求解析式,再求B的坐标;(2)先求点C(0,﹣4),再求直线AC解析式,可设点P(t,﹣
x+b,可求解析式,再求B的坐标;(2)先求点C(0,﹣4),再求直线AC解析式,可设点P(t,﹣![]() t+6),Q(t,
t+6),Q(t,![]() t﹣4),所以d=(﹣
t﹣4),所以d=(﹣![]() t+6)﹣(
t+6)﹣(![]() t﹣4);过点M作MG⊥PQ于G,证△OAC≌△GMQ,得QG=OC=4,GM=OA=8;过点N作NH⊥PQ于H,过点M作MR⊥NH于点R,得四边形GHRM是矩形,得HR=GM=8;设GH=RM=k,由△HNQ≌△RMN,得HN=RM=k,NR=QH=4+k,由HR=HN+NR,得k+4+k=8,可得GH=NH=RM=2,HQ=6,由Q(t,
t﹣4);过点M作MG⊥PQ于G,证△OAC≌△GMQ,得QG=OC=4,GM=OA=8;过点N作NH⊥PQ于H,过点M作MR⊥NH于点R,得四边形GHRM是矩形,得HR=GM=8;设GH=RM=k,由△HNQ≌△RMN,得HN=RM=k,NR=QH=4+k,由HR=HN+NR,得k+4+k=8,可得GH=NH=RM=2,HQ=6,由Q(t,![]() t﹣4),得N(t+2,
t﹣4),得N(t+2,![]() t﹣4+6),代入y=﹣
t﹣4+6),代入y=﹣![]() x+6,得
x+6,得![]() t+2=﹣
t+2=﹣![]() (t+2)+6,求出t=2,再求P(2,
(t+2)+6,求出t=2,再求P(2,![]() ),N(4,3),可得PH=
),N(4,3),可得PH=![]() ,NH=2,最后PN=
,NH=2,最后PN=![]() .
.
解:(1)∵y=﹣![]() x+b交x轴于点A(8,0),
x+b交x轴于点A(8,0),
∴0=﹣![]() ×8+b,b=6,
×8+b,b=6,
∴直线AB解析式为y=﹣![]() x+6,令x=0,y=6,B(0,6);
x+6,令x=0,y=6,B(0,6);
(2)∵A(8,0),B(0,6),
∴OA=8,OB=6,
∵∠AOB=90°,
∴AB=10=BC,
∴OC=4,
∴点C(0,﹣4),设直线AC解析式为y=kx+b’,
∴![]() ,
,
∴ ,
,
∴直线AC解析式为y=![]() x﹣4,
x﹣4,
∵P在直线y=﹣![]() x+6上,
x+6上,
∴可设点P(t,﹣![]() t+6),
t+6),
∵PQ∥y轴,且点Q在y=![]() x﹣4 上,
x﹣4 上,
∴Q(t,![]() t﹣4),
t﹣4),
∴d=(﹣![]() t+6)﹣(
t+6)﹣(![]() t﹣4)=﹣
t﹣4)=﹣![]() t+10;
t+10;
(3)过点M作MG⊥PQ于G,
∴∠QGM=90°=∠COA,
∵PQ∥y轴,
∴∠OCA=∠GQM,
∵CQ=AM,
∴AC=QM,在△OAC与△GMQ中,
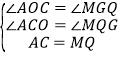 ,
,
∴△OAC≌△GMQ,
∴QG=OC=4,GM=OA=8,过点N作NH⊥PQ于H,过点M作MR⊥NH于点R,
∴∠MGH=∠RHG=∠MRH=90°,
∴四边形GHRM是矩形,
∴HR=GM=8,可设GH=RM=k,
∵△MNQ是等腰直角三角形,
∴∠QMN=90°,NQ=NM,
∴∠HNQ+∠HQN=90°,
∴∠HNQ+∠RNM=90°,
∴∠RNM=∠HQN,
∴△HNQ≌△RMN,
∴HN=RM=k,NR=QH=4+k,
∵HR=HN+NR,
∴k+4+k=8,
∴k=2,
∴GH=NH=RM=2,
∴HQ=6,
∵Q(t,![]() t﹣4),
t﹣4),
∴N(t+2,![]() t﹣4+6)即 N(t+2,
t﹣4+6)即 N(t+2,![]() t+2)
t+2)
∵N在直线AB:y=﹣![]() x+6上,
x+6上,
∴![]() t+2=﹣
t+2=﹣![]() (t+2)+6,
(t+2)+6,
∴t=2,
∴P(2,![]() ),N(4,3),
),N(4,3),
∴PH=![]() ,NH=2,
,NH=2,
∴PN=![]()
=![]() .
.



科目:初中数学 来源: 题型:
【题目】二次函数y=x2+bx的图象如图,对称轴为直线x=1,若关于x的一元二次方程x2+bx﹣t=0(t为实数)在﹣1<x<4的范围内有解,则t的取值范围是( ) 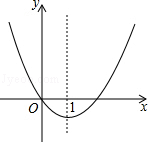
A.t≥﹣1
B.﹣1≤t<3
C.﹣1≤t<8
D.3<t<8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】制造厂的某车间生产圆形铁片和长方形铁片,如图,两个圆形铁片和一个长方形铁片可以制造成一个油桶.已知该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.问安排生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,抛物线y=x2﹣2x与x轴交于O、B两点,顶点为P,连接OP、BP,直线y=x﹣4与y轴交于点C,与x轴交于点D.
(Ⅰ)直接写出点B坐标 ![]() ;判断△OBP的形状
;判断△OBP的形状 ![]() ;
;
(Ⅱ)将抛物线沿对称轴平移m个单位长度,平移的过程中交y轴于点A,分别连接CP、DP;
(i)若抛物线向下平移m个单位长度,当S△PCD= ![]() S△POC时,求平移后的抛物线的顶点坐标;
S△POC时,求平移后的抛物线的顶点坐标;
(ii)在平移过程中,试探究S△PCD和S△POD之间的数量关系,直接写出它们之间的数量关系及对应的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( ) 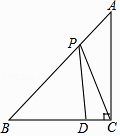
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某张三角形纸片上,取其一边的中点,沿着过这点的两条中位线分别剪去两个三角形,剩下的部分就是如图所示的四边形;经测量这个四边形的相邻两边长为10cm,6cm,一条对角线的长为8cm;则原三角形纸片的周长是_______.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“*”是新规定的这样一种运算法则:a*b=a2+2ab,比如3*(﹣2)=32+2×3×(﹣2)=﹣3
(1)试求2*(﹣3)的值;
(2)若2*x=2,求x的值;
(3)若(﹣2)*(1*x)=x+9,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了形式多样的“阳光体育运动”活动,小李对某班同学参加锻炼的情况进行了统计,并绘制了下面的图1 和图2,并且“乒乓球”对应的∠AOC=108°.
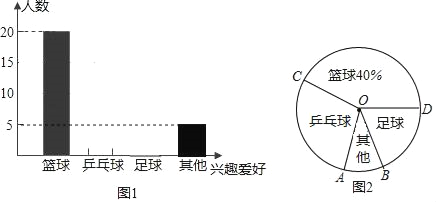
(1)求该班级的学生人数;
(2)在图1中将“乒乓球”和“足球”项目的图形补充完整;
(3)在图2中求∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如同,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由 ![]() ,线段CD和线段BD所围成图形的阴影部分的面积为 .
,线段CD和线段BD所围成图形的阴影部分的面积为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com