
| 工程队 | 每天修路的长度(米) | 单独完成所需天数(天) | 每天所需费用(元) |
| 甲队 | 30 | n | 600 |
| 乙队 | m | n-14 | 1160 |
分析 (1)用总长度÷每天修路的长度可得n的值,继而可得乙队单独完成时间,再用总长度÷乙单独完成所需时间可得乙队每天修路的长度m;
(2)①根据:甲队先修建的长度+(甲队每天修建长度+乙队每天修建长度)×两队合作时间=总长度,列式计算可得;
②由①中的相等关系可得y与x之间的函数关系式;
③根据:甲队先修x米的费用+甲、乙两队每天费用×合作时间≤22800,列不等式求解可得.
解答 解:(1)甲队单独完成这项工程所需天数n=1050÷30=35(天),
则乙单独完成所需天数为21天,
∴乙队每天修路的长度m=1050÷21=50(米),
故答案为:35,50;
(2)①乙队修路的天数为$\frac{1050-90}{30+50}$=12(天);
②由题意,得:x+(30+50)y=1050,
∴y与x之间的函数关系式为:y=-$\frac{1}{80}$x+$\frac{105}{8}$;
③由题意,得:600×$\frac{x}{30}$+(600+1160)(-$\frac{1}{80}$x+$\frac{105}{8}$)≤22800,
解得:x≥150,
答:若总费用不超过22800元,甲队至少先修了150米.
点评 本题主要考查由实际问题抽象出一次函数解析式、一元一次不等式的应用,根据题意完成表格是解题的根本,理解题意得到相等关系或不等关系是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 商品 价格 | A | B |
| 进价(元/件) | m | m+20 |
| 售价(元/件) | 160 | 240 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=2y}\\{2x+3y=7}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x-2y=6}\\{2x+y=12}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{x=6y+2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{-8x+3y=5}\\{8x+9y=1}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,平行四边形ABCD中,AB=2,BC=4,∠ABC=60°,E是BC的中点,点P、Q分别从A、E出发,沿着四边形的边向D点移动,移动时始终保持PQ∥AE,设△BPQ的面积是y,AP=x,则y关于x的函数图象大致是( )
如图,平行四边形ABCD中,AB=2,BC=4,∠ABC=60°,E是BC的中点,点P、Q分别从A、E出发,沿着四边形的边向D点移动,移动时始终保持PQ∥AE,设△BPQ的面积是y,AP=x,则y关于x的函数图象大致是( )| A. | 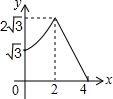 | B. | 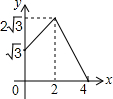 | C. | 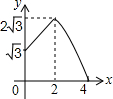 | D. | 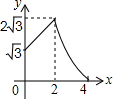 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com