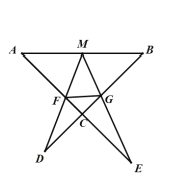
【题目】如图，
为线段
的中点，
与
交于点
，且
交
于
，
交
于
，连
，若
，则
____．
【答案】
【解析】
根据已知条件，∠DME=∠A=∠B=45°，结合三角形外角的性质，即可推出AMF∽△BGM，再根据相似三角形的性质，推出BG的长度，依据锐角三角函数推出AC的长度，即可求出CG、CF的长度，进而推出FG的长度．
解：∵∠AFM=∠DME+∠E（外角定理），
∠DME=∠A=∠B（已知），
∴∠AFM=∠DME+∠E=∠A+∠E=∠BMG，∠A=∠B，
∴△AMF∽△BGM，
∵∠DME=∠A=∠B=45°
∴AC=BC，∠ACB=90°，
∴AC⊥BC，
∵M为AB的中点，
∴AM=BM=
，
∵△AMF∽△BGM，
∴
，
∴
，
AC=BC=
cos45°=4，
∴CG=4-
=
，CF=4-3=1，
在Rt△FCG中，由勾股定理得：
，
故答案为：
新题型全程检测期末冲刺100分系列答案科目：初中数学 来源： 题型：
【题目】“每天锻炼一小时，健康生活一辈子”为了选拔“阳光大课间”领操员，学校组织初中三个年级推选出来的
名领操员进行比赛，成绩如下表：
成绩（分） |
|
|
|
|
人数（人） |
|
|
|
|
（1）这组数据的众数是______，中位数是_______；
（2）已知获得
分的选手中，七、八、九年级分别有
人、
人、人，学校准备从中随机抽取两人领操，求恰好抽到八年级两名领操员的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠B=30°，∠C=45°，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E。若DE=1，则BC的长为（ ）
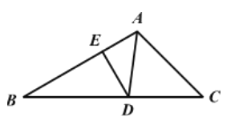
A.2+
B.
C.
D.3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在平面直角坐标系中，点O为坐标原点，直线y＝﹣x+3交x轴于点B，交y轴于点A，过点A作AC⊥AB交x轴于点C．
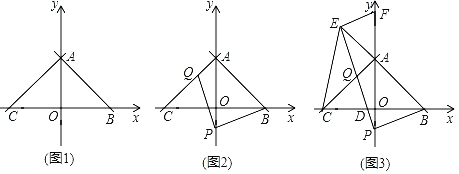
（1）如图1，求直线AC的解析式；
（2）如图2，点P在AO的延长线上，点Q在AC上，连接PB，PQ，且PQ＝PB，设点P的纵坐标为t，AQ的长为d，求d与t之间的函数关系式（不要求写出自变量t的取值范围）；
（3）如图3，在（2）的条件下，PQ交x轴于点D，延长PQ交BA的延长线于点E，过点E作EF⊥PE交y轴于点F，若DE＝
EF，求点Q的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，平面直角坐标系中直线
交坐标轴于
、
两点，抛物线
经过、
两点，点坐标为
．点
为直线
上一点，过点作
轴的垂线，垂足为
，交抛物线于点
．
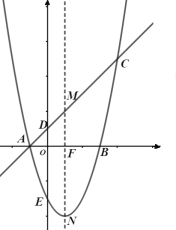
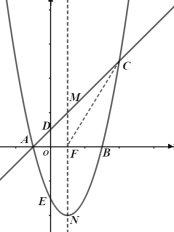
（1）求抛物线的解析式；
（2）是否存在点，使得以点、
、、为顶点的四边形为平行四边形，如果有，求点的坐标，如果没有，请说明理由；
（3）若点在线段上移动时（不含端点），连接
，求
面积的最大值．
查看答案和解析>>
科目：初中数学 来源： 题型：
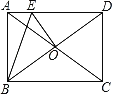
【题目】如图，矩形ABCD的对角线AC与BD交于点O，点E在AD上，且DE＝CD，连接OE，∠ABE＝
∠ACB，若AE＝2，则OE的长为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
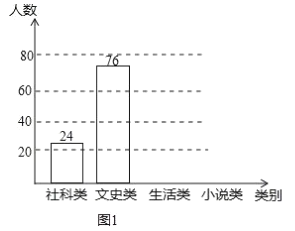
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣，某校为满足学生的阅读需求，欲购进一批学生喜欢的图书，学校组织学生会成员随机抽取部分学生进行问卷调查，被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类，根据调查结果绘制了统计图（未完成），请根据图中信息，解答下列问题
（1）此次共调查了 名学生；
（2）将条形统计图1补充完整；
（3）图2中“社科类”所在扇形的圆心角为 度；
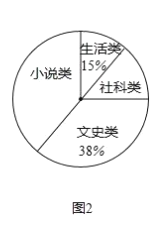
（4）若该校共有学生
人，估计该校喜欢“社科类”书籍的学生人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，E、F分别是正方形ABCD的边BC、CD的中点，连接AF、DE交于点P，过B作BG∥DE交AD于G，BG与AF交于点M．对于下列结论：①AF⊥DE；②G是AD的中点；③∠GBP＝∠BPE；④S△AGM：S△DEC＝1：4．正确的个数是（ ）
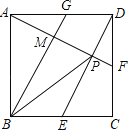
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
