
分析 (1)根据材料直接利用若a与b的积为定值p(p>0),则a+b有最小值2$\sqrt{p}$计算即可;
(2)先用待定系数法求出y与x的函数关系式,再用“均值不等式”,即可得出结论.
解答 解:(1)
∵2x•$\frac{8}{x}$=16,
∴2x+$\frac{8}{x}$≥2$\sqrt{16}$=8,
此时2x=$\frac{8}{x}$,
∴x=2
故答案为:2,8;
(2)∵y1与x-2成正比例函数关系,
∴设y1=k(x-2),
∵y2与x+2成反比例函数关系,
∴y2=$\frac{k'}{x+2}$,
∴y=y1+y2=k(x-2)+$\frac{k'}{x+2}$,
∵当x=6时,y=9;当x=-1时,y=2,
∴$\left\{\begin{array}{l}{k(6-2)+\frac{k'}{6+2}=9}\\{k(-1-2)+\frac{k'}{-1+2}=2}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=2}\\{k'=8}\end{array}\right.$
∴y=2(x-2)+$\frac{8}{x+2}$=2(x+2)+$\frac{8}{x+2}$-8,
∵x>-2,
∴x+2>0,
∴y=2(x+2)+$\frac{8}{x+2}$-8≥2$\sqrt{2(x+2)•\frac{8}{x+2}}$-8≥0,
此时2(x+2)=$\frac{8}{x+2}$,
∴x=-4(舍)或x=0,
即:y的最小值为0.
点评 此题主要考查了待定系数法,正比例函数的定义,反比例函数的定义,待定系数法,材料的理解和掌握,解本题的关键是理解材料提供的信息.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
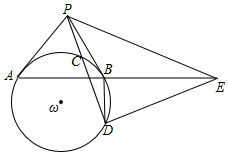 如图,P为圆ω外一点,PA,PB为圆ω的两条切线,PCD为圆ω的一条割线,其中C在线段PD上,直线DE⊥PD交直线AB于点E,求证:∠BPE=2∠PDB.
如图,P为圆ω外一点,PA,PB为圆ω的两条切线,PCD为圆ω的一条割线,其中C在线段PD上,直线DE⊥PD交直线AB于点E,求证:∠BPE=2∠PDB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com