【提出问题】
如图①,在梯形ABCD中,AD//BC,AC、BD交于点E,∠BEC=n°,若AD=a,BC=b,则梯形ABCD的面积最大是多少?
【探究过程】
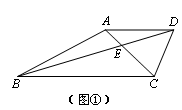
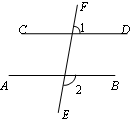
小明提出:可以从特殊情况开始探究,如图②,在梯形ABCD中,AD//BC,AC⊥BD,若AD=3,BC=7,则梯形ABCD的面积最大是多少?
如图③,过点D做DE//AC交BC的延长线于点E,那么梯形ABCD的面积就等于△DBE的面积,求梯形ABCD的面积最大值就是求△DBE的面积最大值.如果设AC=x,BD=y,那么S
△DBE=xy.
以下是几位同学的对话:
A同学:因为y=
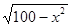
,所以S
△DBE=x
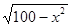
,求这个函数的最大值即可.
B同学:我们知道x
2+y
2=100,借助完全平方公式可求S
△DBE=xy的最大值
C同学:△DBE是直角三角形,底BE=10,只要高最大,S
△DBE就最大,我们先将所有满足BE=10的直角△DBE都找出来,然后在其中寻找高最大的△DBE即可.
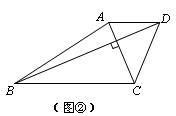
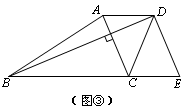
(1)请选择A同学或者B同学的方法,完成解题过程.
(2)请帮C同学在图③中画出所有满足条件的点D,并标出使△DBE面积最大的点D
1.(保留作图痕迹,可适当说明画图过程)
【解决问题】
根据对特殊情况的探究经验,请在图①中画出面积最大的梯形ABCD的顶点D
1,并直接写出梯形ABCD面积的最大值.

 全能测控期末小状元系列答案
全能测控期末小状元系列答案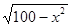 ,所以S△DBE=x
,所以S△DBE=x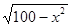 ,求这个函数的最大值即可.
,求这个函数的最大值即可.

