
【题目】某公司研发生产的560件新产品需要精加工后才能投放市场.现由甲、乙两个工厂来加工生产.已知甲工厂每天加工生产的新产品件数是乙工厂每天加工生产新产品件数的1.5倍,并且加工生产240件新产品甲工厂比乙工厂少用4天.
(1)求甲、乙两个工厂每天分别可加工生产多少件新产品?
(2)若甲工厂每天的加工生产成本为3万元,乙工厂每天的加工生产成本为2.4万元,要使这批新产品的加工生产总成本不超过60万元,至少应安排甲工厂加工生产多少天?
【答案】(1)甲工厂每天可以加工生产30件新产品,乙工厂每天可以加工生产20件新产品;(2)至少应安排甲工厂加工生产12天.
【解析】
(1)设乙工厂每天可以加工生产x件新产品,则甲工厂每天可以加工生产1.5x件新产品,根据工作时间=工作总量÷工作效率结合加工生产240件新产品甲工厂比乙工厂少用4天,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设安排甲工厂加工生产m天,则安排乙工厂加工生产(28-1.5m)天,根据总费用=3×甲工厂加工生产的天数+2.4×乙工厂加工生产的天数结合总成本不超过60万元,即可得出关于m的一元一次不等式,解之取其最小值即可得出结论.
(1)设乙工厂每天可以加工生产x件新产品,则甲工厂每天可以加工生产1.5x件新产品,
依题意,得:![]() ,
,
解得:x=20,
经检验,x=20是原分式方程的解,且符合题意,
∴1.5x=30.
答:甲工厂每天可以加工生产30件新产品,乙工厂每天可以加工生产20件新产品.
(2)设安排甲工厂加工生产m天,则安排乙工厂加工生产(28﹣1.5m)天,
依题意,得:3m+2.4(28﹣1.5m)≤60,
解得:m≥12.
答:至少应安排甲工厂加工生产12天.


科目:初中数学 来源: 题型:
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 上的一个动点.
上的一个动点.
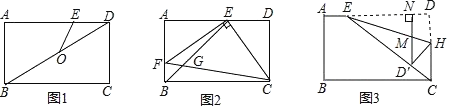
(1)如图1,连接![]() ,
,![]() 是对角线
是对角线![]() 的中点,连接
的中点,连接![]() .当
.当![]() 时,求
时,求![]() 的长;
的长;
(2)如图2,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,与
,与![]() 交于点
交于点![]() .当
.当![]() 平分
平分![]() 时,求
时,求![]() 的长;
的长;
(3)如图3,连接![]() ,点
,点![]() 在
在![]() 上,将矩形
上,将矩形![]() 沿直线
沿直线![]() 折叠,折叠后点
折叠,折叠后点![]() 落在
落在![]() 上的点
上的点![]() 处,过点
处,过点![]() 作
作![]() 于点
于点![]() ,与
,与![]() 交于点
交于点![]() ,且
,且![]() .
.
①求![]() 的值;
的值;
②连接![]() ,
,![]() 与
与![]() 是否相似?请说明理由.
是否相似?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】横店国际马拉松将于2015年5月17日鸣枪开跑,这个赛事的举办掀起了当地跑马拉松的热潮,如图是甲、乙两位马拉松爱好者在一次10公里的“迷你马拉松”训练中两人分别跑的路程y(公里)与时间x(分钟)的函数关系图象,他们同时出发,乙在75分钟的时候到达终点,并在终点等候甲,在甲跑完这个“迷你马拉松”的过程中,(1)甲前半程的速度是![]() 公里/分;(2)乙在冲刺阶段的速度
公里/分;(2)乙在冲刺阶段的速度![]() 公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距0.1公里的次数是4次.以上说法正确的个数是( )
公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距0.1公里的次数是4次.以上说法正确的个数是( )
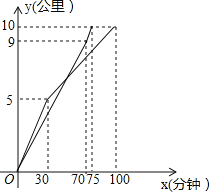
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,反比例函数
,反比例函数![]() (
(![]() )的图像与矩形两边AB、BC分别交于点D、点E,且
)的图像与矩形两边AB、BC分别交于点D、点E,且![]() .
.
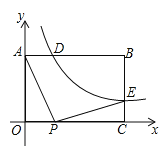
(1)求点D的坐标和![]() 的值;
的值;
(2)求证:![]() ;
;
(3)若点![]() 是线段
是线段![]() 上的一个动点,是否存在点
上的一个动点,是否存在点![]() ,使
,使![]() ?若存在,求出此时点
?若存在,求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
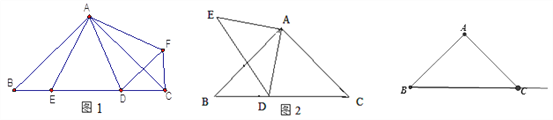
【题目】(1)如图1,在Rt△ABC 中, ![]() ,D、E是斜边BC上两动点,且∠DAE=45°,将△
,D、E是斜边BC上两动点,且∠DAE=45°,将△![]() 绕点
绕点![]() 逆时针旋转90后,得到△
逆时针旋转90后,得到△![]() ,连接
,连接![]() .
.
(1)试说明:△![]() ≌△
≌△![]() ;
;
(2)当BE=3,CE=9时,求∠BCF的度数和DE的长;
(3)如图2,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,D是斜边BC所在直线上一点,BD=3,BC=8,求DE2的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为更好地开展“传统文化进校园”活动,随机抽查了部分学生,了解他们最喜爱的传统文化项目类型(分为书法、围棋、戏剧、国画共4类),并将统计结果绘制成如图不完整的频数分布表及频数分布直方图.
最喜爱的传统文化项目类型频数分布表


根据以上信息完成下列问题:
(1)直接写出频数分布表中a的值;
(2)补全频数分布直方图;
(3)若全校共有学生1500名,估计该校最喜爱围棋的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了预测本校九年级男生毕业体育测试达标情况,随机抽取该年级部分男生进行一次测试(满分50分,成绩均记为整数分),并按测试成绩m(单位:分)分类:A类(45<m≤50),B类(40<m≤45),C类(35<m≤40),D类(m≤35)绘制出如图所示的不完整条形统计图,请根据图中信息解答下列问题:
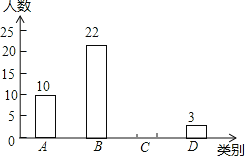
(1)a= ,b= ,c= ;
成绩等级 | 人数 | 所占百分比 |
A类(45 | 10 | 20% |
B类 | 22 | 44% |
C类 | a | b |
D类 | c |
(2)补全条形统计图;
(3)若该校九年级男生有600名,D类为测试成绩不达标,请估计该校九年级男生毕业体育测试成绩能达标的有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com