
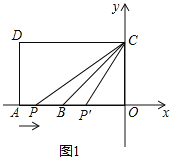
【题目】如图,A(﹣5,0),B(﹣3,0)点C在y的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°,点P从点A出发,沿x轴向右以每秒1个单位长度的速度运动,运动时间为t秒.
(1)当时t=1,求PC的长;
(2)当∠BCP=15°时,求t的值;
(3)以线段PC为直径的⊙Q随点P的运动而变化,当⊙Q与四边形ABCD的边(或边所在的直线)相切时,求t的值.

【答案】(1)PC=5;(2)当∠BCP=15°时,t的值为(5﹣3![]() )秒或(5﹣
)秒或(5﹣![]() )秒;(3)t的值为8秒或5秒或
)秒;(3)t的值为8秒或5秒或![]() 秒.
秒.
【解析】
(1)由题意可知△BOC是等腰直角三角形,由此即可解决问题.
(2)分两种情形①当点P在点B右侧时,②当点P′在点B左侧时,分别解直角三角形即可.
(3)由题意知,若该圆与四边形ABCD的边相切,有三种情况:①当该圆与BC相切于点C时.②当该圆与CD相切于点C时.③当该圆与AD相切时;分别解直角三角形,求出AP的长即可解决问题.
(1)A(﹣5,0),B(﹣3,0),
∴OA=5,OB=3,
当t=1时,AP=1,
∴OP=OA﹣AP=4,
∵∠CBO=45°,∠BOC=90°,
∴△BOC是等腰直角三角形,
∴∠OCB=45°,OC=OB=3,
∴PC=![]() =5;
=5;
(2)分两种情况:如图1所示:①当P在点B的左侧时,
∵∠CBO=45°,∠BCP=15°
∴∠OCP=∠OCB+∠BCP=45°+15°=60°,
∴∠OPC=30°,
∴OP=![]() OC=3
OC=3![]() ,
,
∴AP=OA﹣OP=5﹣3![]() ,
,
∵点P沿x轴向右以每秒1个单位的速度运动,
∴t=5﹣3![]() ,
,
②当![]() 在点B的右侧时,
在点B的右侧时,
∵∠OCB=45°,∠BC![]() =15°
=15°
∴∠OC![]() =∠OCB﹣∠BC
=∠OCB﹣∠BC![]() =45°﹣15°=30°,
=45°﹣15°=30°,
∴O![]() =
=![]() OC=
OC=![]() ,
,
∴A![]() =OA﹣O
=OA﹣O![]() =5﹣
=5﹣![]() ,
,
∵点![]() 沿x轴向右以每秒1个单位的速度运动,
沿x轴向右以每秒1个单位的速度运动,
∴t=5﹣![]() ;
;
综上所述,当∠BCP=15°时,t的值为(5﹣3![]() )秒或(5﹣
)秒或(5﹣![]() )秒;
)秒;
(3)如图2中,由题意知,若该圆与四边形ABCD的边相切,有以下三种情况:
①当该圆与BC相切于点C时,有∠BCP=90°,
从而∠OCP=45°,得到OP1=OC=3,此时AP1=5+3=8,
∴t=8;
②当该圆与CD相切于点C时,有P2C⊥CD,即点P2与点O重合,
此时AP2=5,
∴t=5;
③当该圆与AD相切时,
设P3(5﹣t,0),则Q(![]() ,
,![]() ),半径r2=(
),半径r2=(![]() )2+(
)2+(![]() )2,
)2,
作QH⊥AD于点H,则QH=![]() ,
,
∵QH2=r2,
∴(![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,
)2,
解得t=![]() ,
,
综上所述,t的值为8秒或5秒或![]() 秒.
秒.



 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
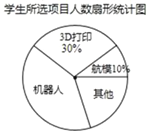
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.
男、女生所选项目人数统计表
项目 | 男生(人数) | 女生(人数) |
机器人 | 7 | 9 |
3D打印 | m | 4 |
航模 | 2 | 2 |
其他 | 5 | n |
根据以上信息解决下列问题:
(1)m= ,n= ;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 °;
(3)从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
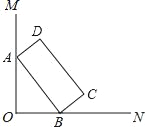
【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.
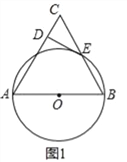

(1)试判断△ABC的形状,并说明理由;
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=![]() ,求⊙O的半径和BF的长
,求⊙O的半径和BF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了参加中考体育测试,甲,乙,丙三位同学进行足球传球训练.球从一个人脚下随机传到另一个人脚下,且每位传球人传球给其余两人的机会是均等的,由甲开始传球,共传三次.
(1)求请用树状图列举出三次传球的所有可能情况;
(2)传球三次后,球回到甲脚下的概率;
(3)三次传球后,球回到甲脚下的概率大还是传到丙脚下的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2﹣(3a+1)x+2a+1(a≠0),与x轴交与A(x1,0)B(x2,0)两点,与y轴交与C点.
(1)求出该函数的图象经过的定点的坐标.
(2)若A为(1)中所求的某一定点,且x1、x2,之间的整数恰有3个(不包括x1、x2),试求a的取值范围.
(3)当a=![]() 时,将与x轴重合的直线绕着D(﹣5,0)逆时针旋转得到直线l:y=kx+b,过点C、B分别作l的垂线段,距离为d1、d2,试分别求出当|d1﹣d2|最大和最小时b的值.
时,将与x轴重合的直线绕着D(﹣5,0)逆时针旋转得到直线l:y=kx+b,过点C、B分别作l的垂线段,距离为d1、d2,试分别求出当|d1﹣d2|最大和最小时b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
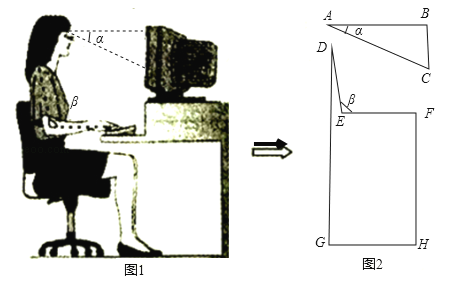
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点![]() 和
和![]() ,给出如下定义:若
,给出如下定义:若![]() ,则称点Q为点P的“可控变点”.
,则称点Q为点P的“可控变点”.
例如,点![]() 的“可控变点”为点
的“可控变点”为点![]() ,点
,点![]() 的“可控变点”为点
的“可控变点”为点![]() .
.
(1)点![]() 的“可控变点”坐标为 ;
的“可控变点”坐标为 ;
(2)若点P在函数![]() 的图象上,其“可控变点”Q的纵坐标
的图象上,其“可控变点”Q的纵坐标![]() 是7,求“可控变点” Q的横坐标;
是7,求“可控变点” Q的横坐标;
(3)若点P在函数![]() 的图象上,其“可控变点”Q的纵坐标
的图象上,其“可控变点”Q的纵坐标![]() 的取值范围是
的取值范围是![]() ,直接写出实数a的值.
,直接写出实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
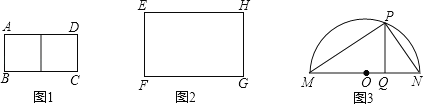
【题目】(1)如图1,矩形ABCD是由两个边长为1的正方形构成.请你剪两刀后拼成一个与矩形ABCD面积相等的正方形.
(2)如图2,矩形EFGH的长FG为6,宽EF为4,用剪刀剪两次,然后将其拼接成一个与矩形EFGH面积相等的正方形,画出裁剪线及拼接后的图形,简要说明裁剪线是如何确定的.如果你没有想到好方法,不用急,请沉着应对.细读下列数学事实或许对你解决有帮助.
(3)如图3,在⊙O中,MN为直径,PQ⊥MN,垂足为点Q,交⊙O于点P,连结PM、PN.易证明PQ2=MQNQ.此结论可直接运用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com